分子動力学計算の実践講習 −溶融塩とイオン液体−
第48回溶融塩講習会は終了しました。多数のご参加、ありがとうございました。
日時: 2019年11月19日(火) 9:00〜18:00 【事前講習会11月18日(月)13:00〜18:00】
場所: 千葉大学西千葉キャンパス (東京駅から最寄りのJR西千葉駅まで1時間弱)
会場: 千葉大学ベンチャービジネスラボラトリ3階会議室 (JR西千葉駅から徒歩5分) 学内地図
担当: 千葉大学大学院工学研究院 大窪 貴洋
申し込み方法や参加費の支払い方法などは、(社)電気化学会溶融塩委員会 溶融塩化学講習会のページを御覧ください。
注意事項
はじめに
材料の分子構造や物性を予測するため、計算機シミュレーションがあたりまえ のように使われてきています。特に溶融塩やイオン液体のように高温下や不活 性雰囲気での取扱いを必要とし、実験することが容易でない材料の特性や分子 構造を調べるために計算機シミュレーションは有用です。溶融塩分野での計算 機シミュレーションは、原子・電子構造解析から反応炉の設計まで幅広く用い られていますが、本講習会では溶融塩の物性予測や分子構造の解析に有用な分 子動力学計算を取り扱います。本講習会は、分子動力学計算の初学者を対象と し、参加者が次の項目を達成できるよう講習します。
- 分子動力学計算の基本原理を理解する。
- 論文や書籍の分子動力学計算を自分でトレースできるようになる。
- 組成や温度をパラメータとしたシミュレーションを行い溶融塩の物性を予測する。
現在、分子動力学計算を行うソフトウェアは無料のものから有料のものまで多 数存在します。シミュレーションの実行環境もデスクトップPCから大型の並列 計算機からまで多岐にわたります。本講習会の達成目標を考慮すると、試行錯 誤を何度も繰り返してシミュレーションを行い、理解を深めてもらった方が望 ましいので、自前のPCを使って講習することとします。また分子シミュレーショ ンコードとして、学術研究や企業の研究開発でもよく用いられているLAMMPSを 用います。LAMMPSは、デスクトップPCから大型の並列計算機まで環境を選ばず 実行できますので、自前のPCで慣れてきたら大型の計算機上へ実行環境を移行 することもスムーズかと思います。またGUIを搭載した以下の分子動力学計算 用プリ・ポスト処理ソフトウェアは分子動力学計算としてLAMMPSを利用して います。
このようなプリ・ポスト処理ソフトウェアを利用して計算を行う場合でも LAMMPSをよく理解してシミュレーションを行うことは、動作原理を理解する上 でも有用と思います。またプリポスト用ソフトウェアで対応していないLAMMPS の機能や、最新のLAMMPSバージョンを利用したい場合は、LAMMPSを直接実行す る必要がありますので、LAMMPSの使い方を覚えておいて損はありません。
本講習会では、LAMMPSのインプット・アウトプットファイルの形式を理解し、 自前のPCで結晶構造や分子構造、ガラス組成からMD計算をスタートする方法を 説明します。また大型の並列計算機が一般にLinux等のUNIX環境であることか ら、Linux環境でのシミュレーションを講習します。講習会では、Linuxや LAMMPSのセットアップは行いませんので、自力での構築が難しい場合は、事前 講習会に参加してください。
講習会スケジュール
進行具合を確認しながら進めますので、タイムテーブルはあくまで予定です。
| 9:00 | 9:05 | 講習会はじまりの挨拶 |
| 9:00 | 10:00 | 分子動力学計算、LAMMPSコードについて (講習) |
| 10:00 | 11:00 | LAMMPSの実行、インプット・アウトプットについて (講習・実習) |
| 11:00 | 12:00 | 液体Arの分子動力学計算 (講習・実習) |
| 12:00 | 13:00 | 昼休み |
| 13:00 | 14:30 | 溶融塩のシミュレーション (講習・実習) |
| 14:30 | 16:00 | イオン液体のシミュレーション (講習・実習) |
| 16:00 | 17:30 | インプットファイルの作成、シミュレーションの実行 (自由課題) |
分子動力学計算の基本
分子動力学計算の基礎的事項の講義
分子動力学計算の基本的な理論と計算技法について以下の項目の講義を行います。
- 分子動力学計算の歴史
- 速度Verlet法
- 周期境界条件
- ポテンシャル関数
- アンサンブル
分子構造やダイナミクスを評価うするため動径分布関数や平均自乗変位につい て講義します。また、分子動力学計算からマクロな物性を評価するための自己 相関関数の考え方についても講義します。
- 動径分布関数
- 平均自乗変位
- 自己相関関数
LAMMPSコードについて
LAMMPSコードについて、その特徴と構成について簡単に説明します。
- コードの特徴
- ソースコードの構成
液体Ar
液体Arの分子動力学計算を行った論文を取り上げ内容を解説した後、論文と同様のMD計算を行い、液体Ar構造の可視化、密度評価、動径分布関数による構造評価、ダイナミクスとして平均自乗変位から自己拡散係数を求めます。
初期構造の作成
Arの密度からセルを作る。ポテンシャル関数の変数も定義する。
Liquid Ar (rho=1.374g/cm3), Phys. Rev. 136, A405 (1964) 1 atoms 1 atom types 0 3.6412664191749493 xlo xhi 0 3.6412664191749493 ylo yhi 0 3.6412664191749493 zlo zhi Masses 1 39.948 Pair Coeffs # lj/cut 1 0.23846475655872523 3.4 Atoms 1 1 0.0 0.0 0.0
平衡計算と動径分布関数と平均自乗変位の計算
- 10x10x10のセル(1000個のAr)としNVT(94.4K)とする。
- 3 psの計算で平衡状態を得る。
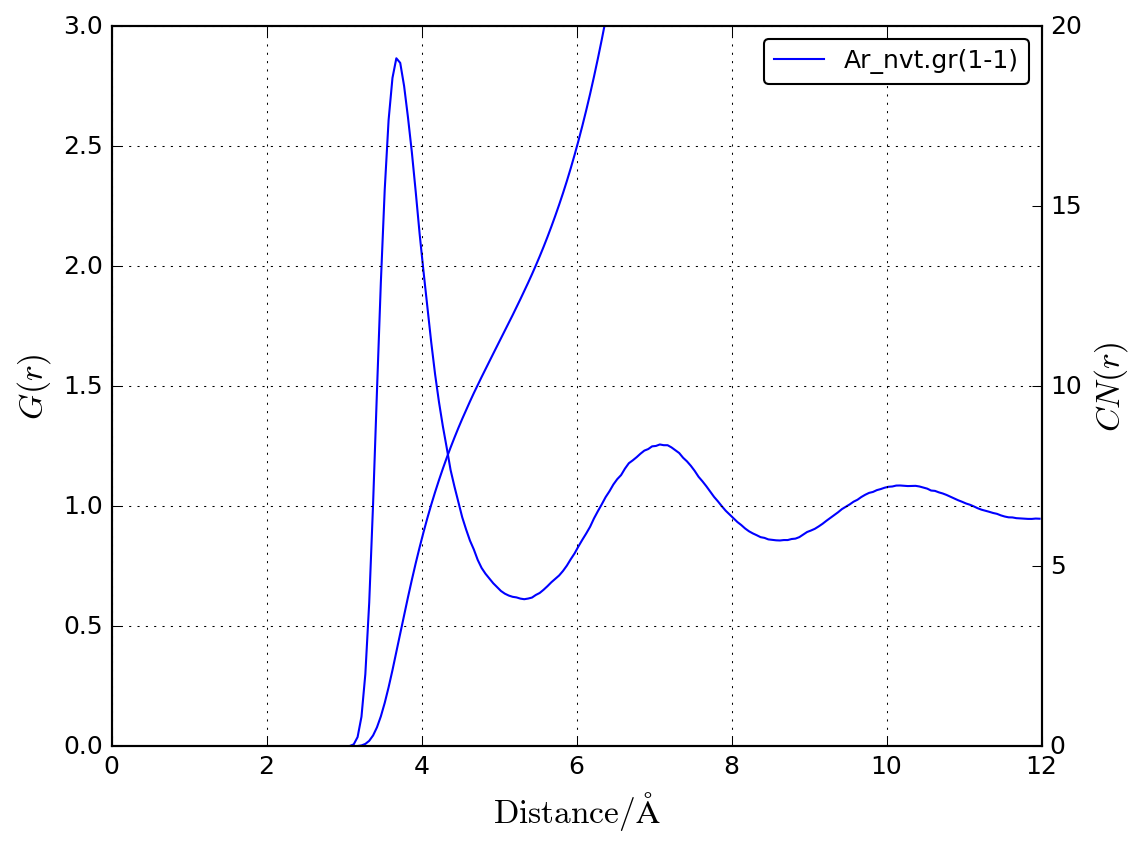
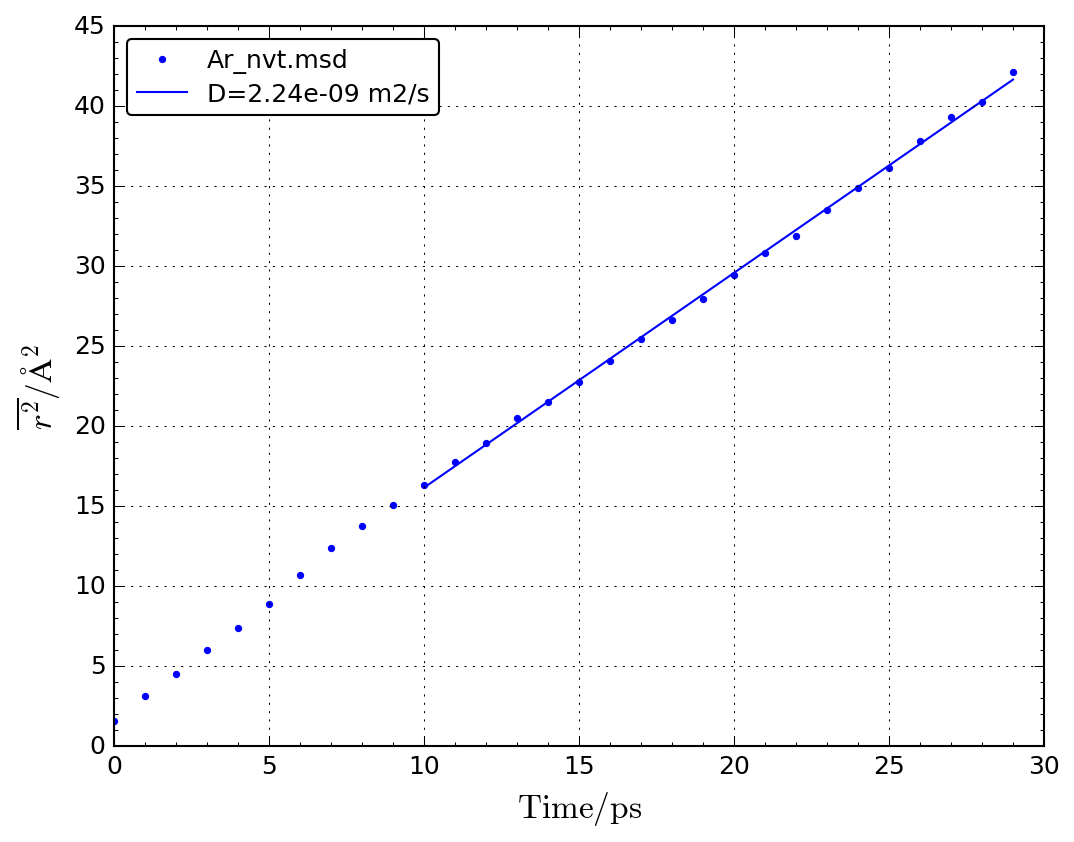
- 30 psの計算で動径分布関数と平均自乗変位を計算する。
- 動径分布関数は12 Åまで計算する。
- 平均自乗変位は1 ps毎に計算する。
計算を実行します(Total wall time: 0:00:05)。
mpirun -np 4 lammps -in Ar_nvt.in -log Ar_nvt.log
# Correlations in the Motion of Atoms in Liquid Argon # A. Rahman, Phys. Rev. 136, A405 (1964) # 単位の指定(E:kcal/mol, time:fs, distance:Ang., mass:g/mol, P:atmospheres) units real # ポテンシャル関数とcutoff距離 (# https://lammps.sandia.gov/doc/pair_lj.html) pair_style lj/cut 7.65 # simulation boxとポテンシャル関数の係数をAr.dataから読む read_data Ar.data # 10x10x10のスーパーセルを生成, 10*10*10=1,000個のAr replicate 10 10 10 # 熱力データを出力頻度(10ステップ毎)と出力パラメータ thermo 10 thermo_style custom step temp etotal press vol density # 粒子に与える温度(初期速度)と乱数用のseed velocity all create 94.4 777 # NVTアンサンブルで温度は94.4K fix 1 all nvt temp 94.4 94.4 100 # 100step毎に粒子の座標をAr.lammpstrjに記録 dump 1 all custom 1 Ar_nvt.lammpstrj id element x y z # 原子番号でsortして元素記号を付したlammpstrjを保存 dump_modify 1 element Ar sort id # 計算の時間刻み 1 fs timestep 10 # 300ステップ=3ps実行して系を平衡にする run 300 # 平衡になったら動径分布関数と平均自乗変位の計算 comm_modify cutoff 14 compute a all rdf 240 * * cutoff 12 fix 2 all ave/time 1 100 100 c_a[*] file Ar_nvt.gr mode vector compute b all msd fix 3 all ave/time 1 1 100 c_b[*] file Ar_nvt.msd title1 "#dt=10fs" run 3000
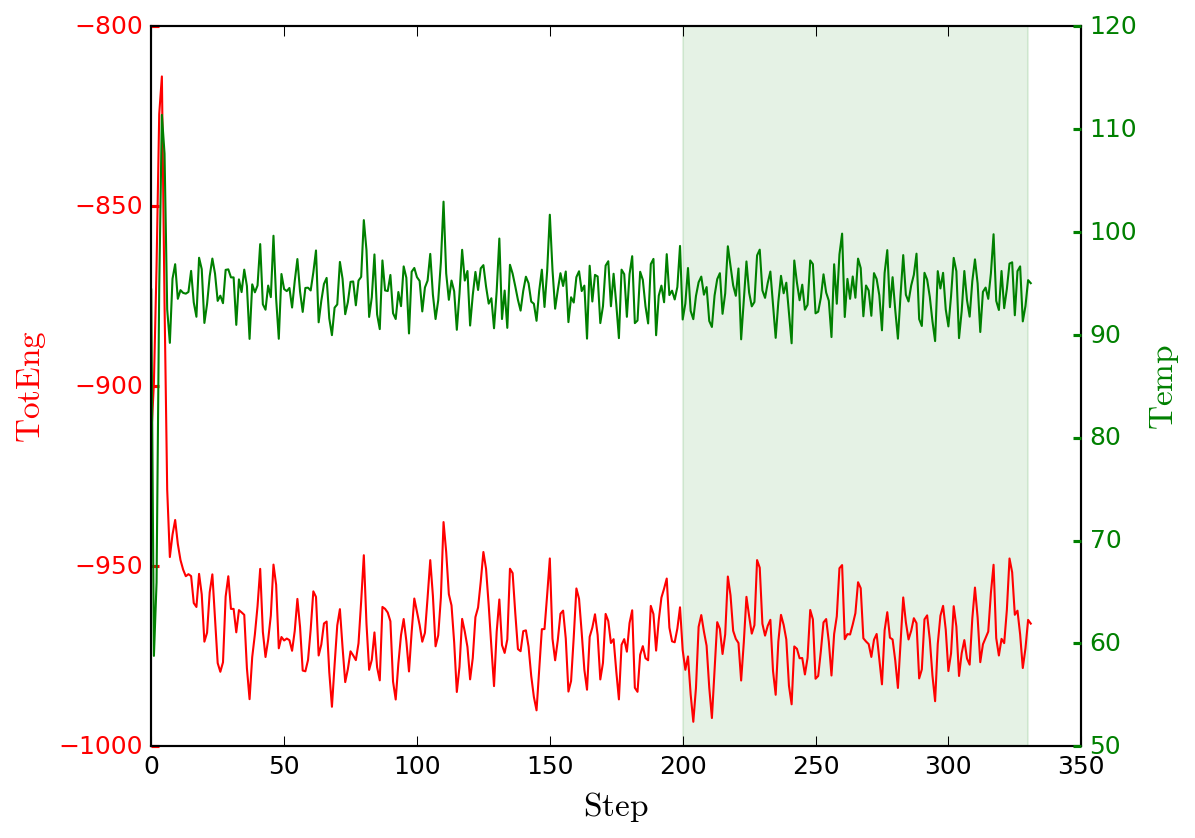
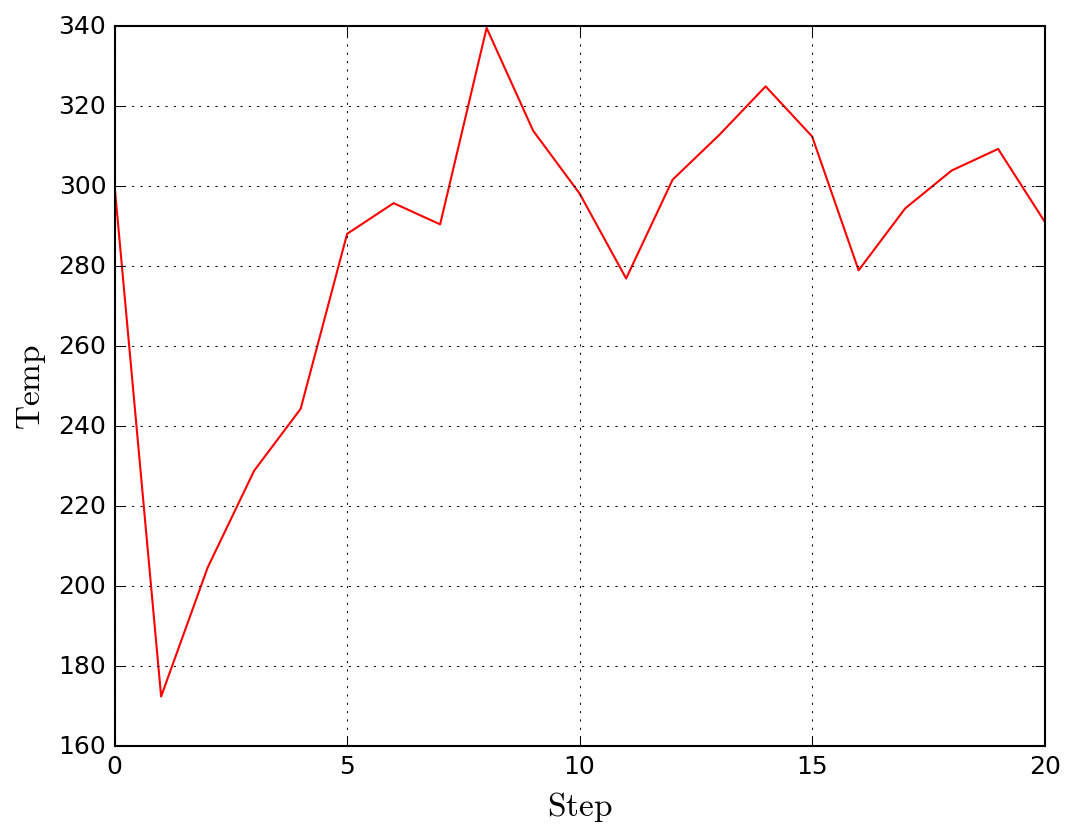
平衡状態を確認し、200ステップから330ステップ(20から33 ps)の範囲で平均 エネルギーと密度を計算します。
logplot.py Ar_nvt.log -k TotEng Temp -w 200 330 -o log.png
エネルギーと密度が得られます。
Total run: 2 keywords: [Step, Temp, TotEng, Press, Volume, Density] Ar_nvt.log: TotEng = -966.261 +/- 9.10696 Ar_nvt.log: Temp = 94.5187 +/- 2.50601
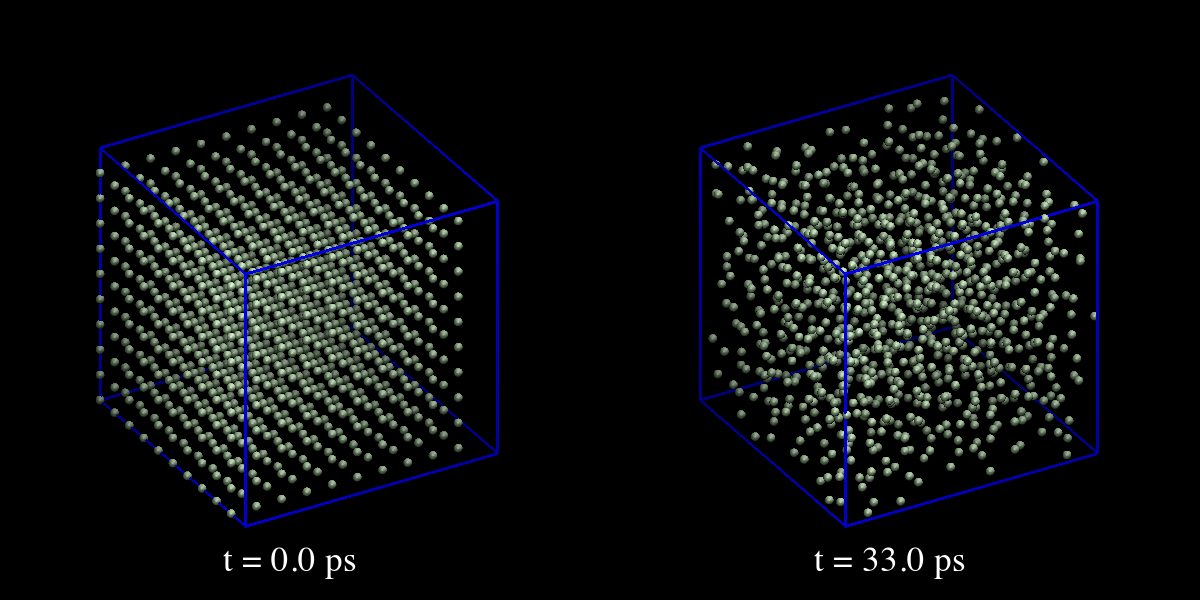
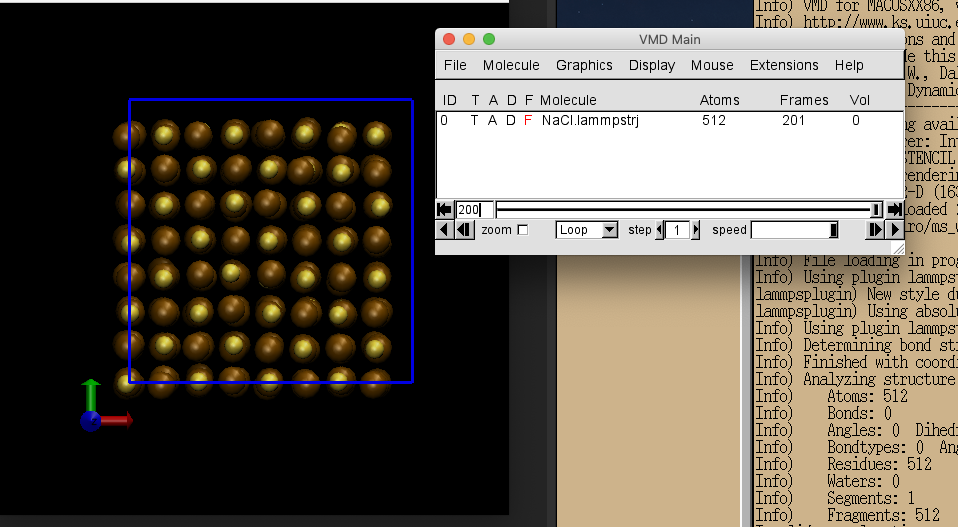
VDMで初期構造から最終ステップまでの構造を可視化して確認します。
固体・溶融NaCl
MD計算による溶融NaClの熱伝導率を計算した論文を取り上げポテンシャル関数等を解説した後、NaClのMD計算を行います。構造やダイナミクスを評価するとともに熱伝導率を計算します。
初期構造の作成
NaClの結晶構造データ(Crystallographic Information File; CIF)からNaClの結晶データを取得し初期構造を作成します。
COMMENT 8 atoms 2 atom types 0.0 5.620 xlo xhi 0.0 5.620 ylo yhi 0.0 5.620 zlo zhi PairIJ Coeffs 1 1 6.081 0.31700 2.340 24.18024 -11.5120 1 2 4.864 0.31700 2.755 161.2016 -200.02100 2 2 3.649 0.31700 3.170 1669.588 -3352.8700 Masses 1 22.989768 2 35.4527 Atoms 1 1 +1.0 0.000000 0.000000 0.000000 # Na 2 1 +1.0 0.000000 2.810000 2.810000 # Na 3 1 +1.0 2.810000 0.000000 2.810000 # Na 4 1 +1.0 2.810000 2.810000 0.000000 # Na 5 2 -1.0 2.810000 2.810000 2.810000 # Cl 6 2 -1.0 2.810000 0.000000 0.000000 # Cl 7 2 -1.0 0.000000 2.810000 0.000000 # Cl 8 2 -1.0 0.000000 0.000000 2.810000 # Cl
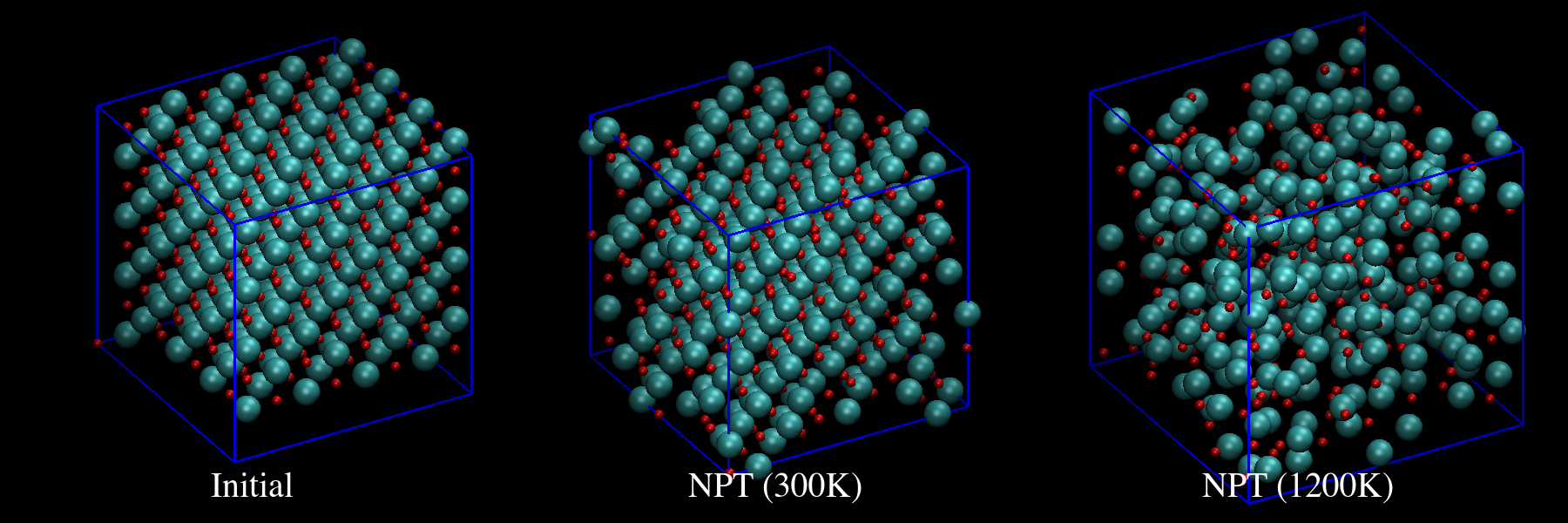
初期構造から次のステップで計算を行って、300Kと1200KのMD計算を行います。
units real
pair_style born/coul/long 10
kspace_style ewald 1.0e-5
atom_style charge
read_data NaCl.data
replicate 4 4 4
group Na type 1
group Cl type 2
thermo 100
thermo_style custom step temp etotal press vol density
variable dt equal 2.0
variable title format dt "#dt=%.8gfs;"
timestep ${dt}
# 300 K equilibrium
variable T equal 300
velocity all create ${T} 777
fix 1 all npt temp ${T} ${T} 100 iso 1 1 1000
dump 1 all custom 10 NaCl.lammpstrj id type element x y z
dump_modify 1 element Na Cl sort id
run 1000
# 300 K sampling
compute 1 Na msd
compute 2 Cl msd
compute 3 all rdf 200 1 2
fix 2 all ave/time 1 1 5 c_1[*] &
file Na_${T}K.msd title1 ${title}
fix 3 all ave/time 1 1 5 c_2[*] &
file Cl_${T}K.msd title1 ${title}
fix 4 all ave/time 1 100 100 c_3[*] &
file NaCl_${T}K.gr mode vector title1 "#PAIRS=Na-Cl"
run 10000
uncompute 1
uncompute 2
uncompute 3
unfix 2
unfix 3
unfix 4
# build melt structure
# 2000K->1200K
variable T equal 1200
fix 1 all npt temp 2000 2000 100 iso 1 1 1000
run 1000
fix 1 all npt temp 2000 ${T} 100 iso 1 1 1000
run 1000
# 1200K
fix 1 all npt temp ${T} ${T} 100 iso 1 1 1000
run 1000
compute 1 Na msd
compute 2 Cl msd
compute 3 all rdf 200 1 2
fix 2 all ave/time 1 1 5 c_1[*] &
file Na_${T}K.msd title1 ${title}
fix 3 all ave/time 1 1 5 c_2[*] &
file Cl_${T}K.msd title1 ${title}
fix 4 all ave/time 1 100 100 c_3[*] &
file NaCl_${T}K.gr mode vector title1 "#PAIRS=Na-Cl"
run 10000
write_data NaCl_1200K.data pair ij
計算を実行します(Total wall time: 0:01:06)。
mpirun -np 4 lammps -in NaCl.in -log NaCl.log
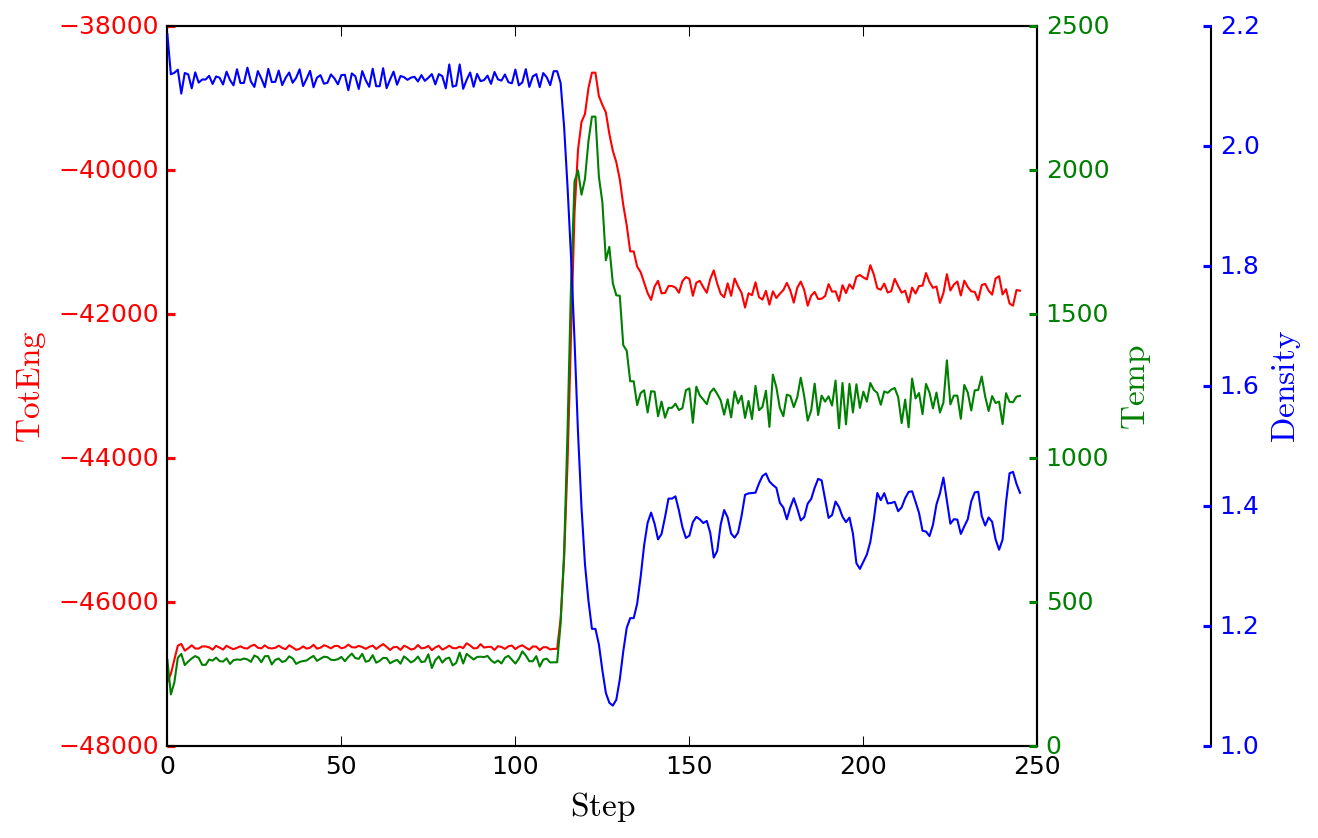
MD計算でのエネルギーと温度、密度変化を確認します。
logplot.py NaCl.log -k TotEng Temp Density
構造とダイナミクス評価
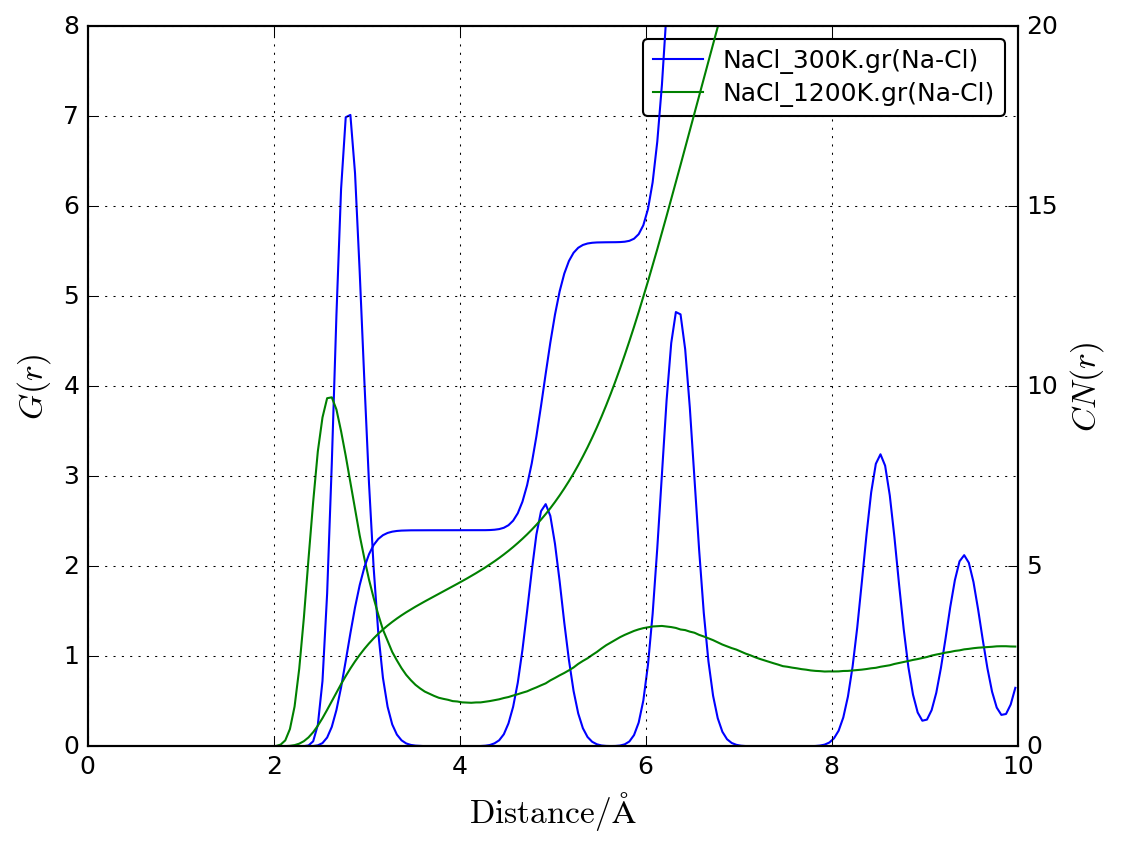
動径分布関数をプロットします。
grplot.py NaCl_300K.gr NaCl_1200K.gr -o gr.png
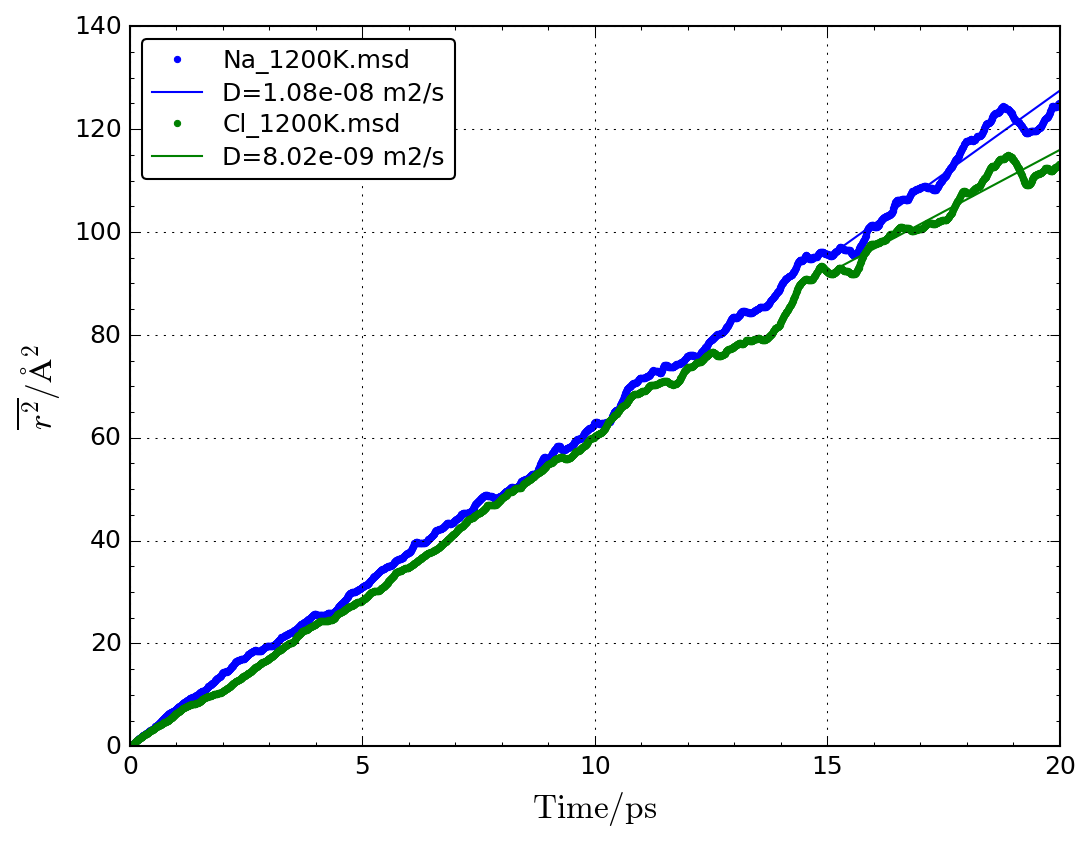
NaとClの平均自乗変位をプロットして、15から20 psの範囲で直線を引き傾きより拡散係数します。
msdplot.py Na_1200K.msd Cl_1200K.msd -w 15 20
やや統計精度が悪いですが、1200 KでのNaとClの拡散係数が求まります。
Na_1200K.msd: D=1.26e-08 m2/s Cl_1200K.msd: D=1.08e-08 m2/s
熱伝導率の計算
保存した1,200Kでのデータを読んでフラックスの計算します。
variable T equal 1200 # temperature
variable dt equal 2 # timestep
variable V equal vol # volume
units real
pair_style born/coul/long 10
kspace_style ewald 1.0e-5
atom_style charge
read_data NaCl_${T}K.data
thermo 100
thermo_style custom step temp etotal press vol density
# make title header in flux output file
variable dt_ format dt "dt=%.8gfs"
variable T_ format T "T=%.8gK"
variable V_ format V "V=%.8gAng3"
variable title string "#${dt_};${T_};${V_};[Kappa_calc.]"
timestep ${dt}
velocity all scale ${T}
fix 1 all nve
# compute energy flux
compute myKE all ke/atom
compute myPE all pe/atom
compute myStress all stress/atom NULL virial
compute flux all heat/flux myKE myPE myStress
variable Jx equal c_flux[1]/$V
variable Jy equal c_flux[2]/$V
variable Jz equal c_flux[3]/$V
# save flux data every step
fix 2 all print 1 "$(step) ${Jx} ${Jy} ${Jz}" &
title ${title} screen no file NaCl_${T}K.flux
run 10000
計算を実行します(Total wall time: 0:00:59)。
mpirun -np 4 lammps -in NaCl_kappa.in -log NaCl_kappa.log
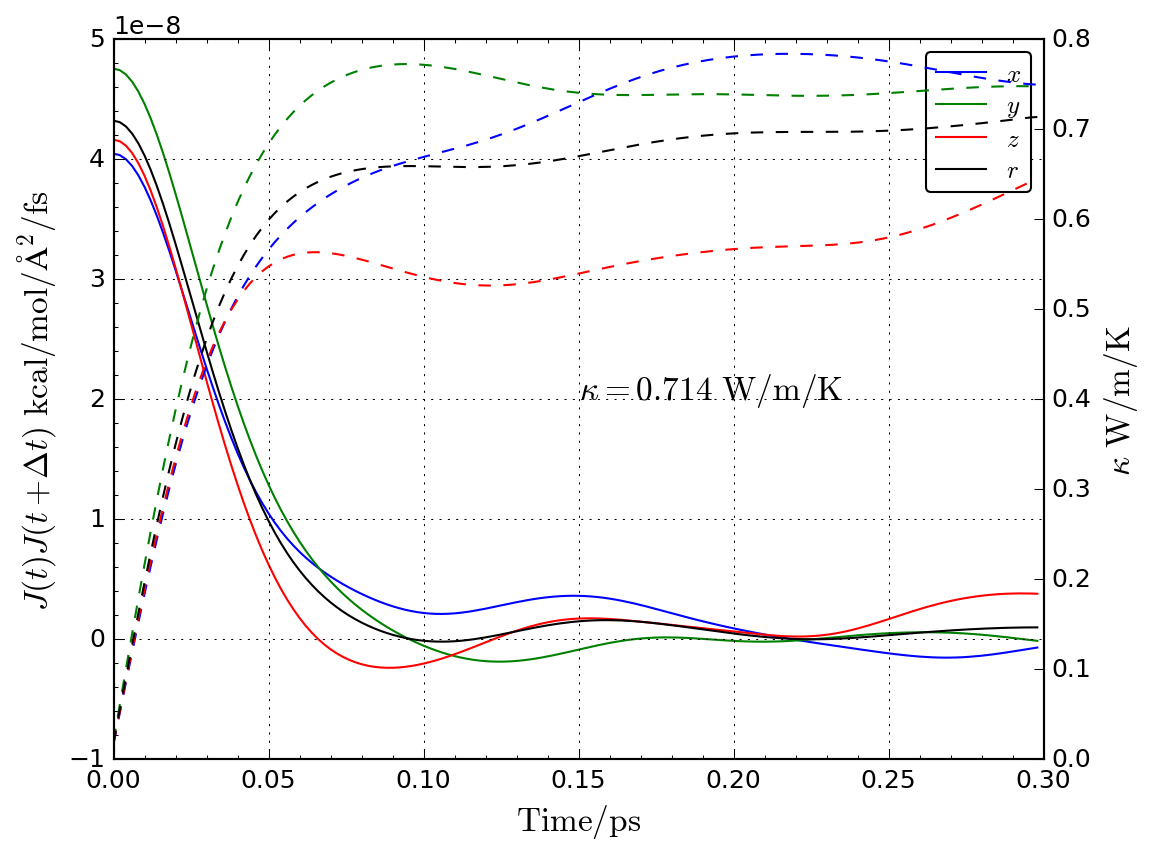
0.3 psの時間windowで相関関数を計算して積分し熱伝導率を求めます。積分 値が収束するよう相関時間の窓を0.3 psとして相関関数を求めます。また相 関関数を計算するための時間シフトは1ステップとします。
corrplot.py NaCl_1200K.flux -s 1 -w 0.3
0.3 psの時間widowsから求めた積分結果は、やや収束していませんが熱伝導率 が求まります。
kappa = 0.610108 W/m/K kappa_xx = 0.859257 W/m/K kappa_yy = 0.546289 W/m/K kappa_zz = 0.424778 W/m/K
emim-ntf2イオン液体
イオン液体のMD計算の論文(カチオン)とアニオンを参考にポテンシャル関数等 を解説した後、1-ethyl-3-methylimidazolium (c2c1im)と trifluoromethylsufate (ntf2)からなるイオン液体のMD計算を行います。構造 やダイナミクスを評価するとともに粘性係数を計算します。
初期構造の作成と平衡計算
分子系のインプットファイルは、各分子の結合距離や角度、二面角等を指定す る必要があります。分子系のインプットファイルを手作業で作成することは、 あまりにつらいので配布したスクリプトで作成します。c2c1imとntf2が27個ず つからなるセルのインプットファイルを以下のコマンドで生成します。
make_il.py --c2c1im 27 --ntf2 27 -o emim-ntf2
このコマンドで以下の2つのファイルが生成されます。
- emim-ntf2.data
emim-ntf2.in
# 27c2c1im-27ntf2 units real atom_style full pair_style lj/cut/coul/long 12.0 12.0 pair_modify mix geometric tail yes kspace_style ewald 1.0e-5 variable T equal 300 special_bonds lj/coul 0.0 0.0 0.5 bond_style harmonic angle_style harmonic dihedral_style opls improper_style cvff read_data emim-ntf2.data thermo 100 thermo_style custom step temp etotal press vol density timestep 1.0 velocity all create 2000 777 dump 1 all custom 100 emim-ntf2.lammpstrj & id mol type element x y z dump_modify 1 element C C C C H H H H N C F N O S sort id fix SHAKE all shake 0.0001 20 0 b 1 5 7 fix DEFORM all deform 1 & x scale 0.5000 y scale 0.5000 z scale 0.5000 fix 1 all nvt temp 2000 2000 100 run 3000 unfix DEFORM kspace_style pppm 1.0e-5 run 3000 fix 1 all nvt temp 2000 ${T} 10 run 3000 unfix 1 fix 1 all npt temp ${T} ${T} 100 iso 1 1 1000 run 10000 write_data emim-ntf2_eq.data
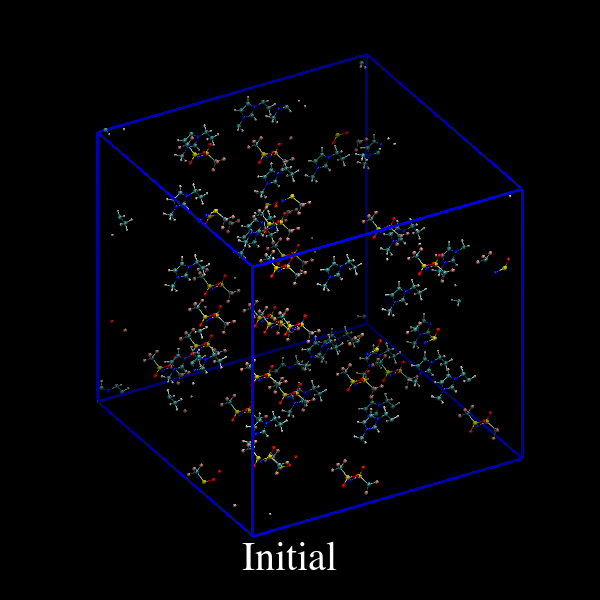
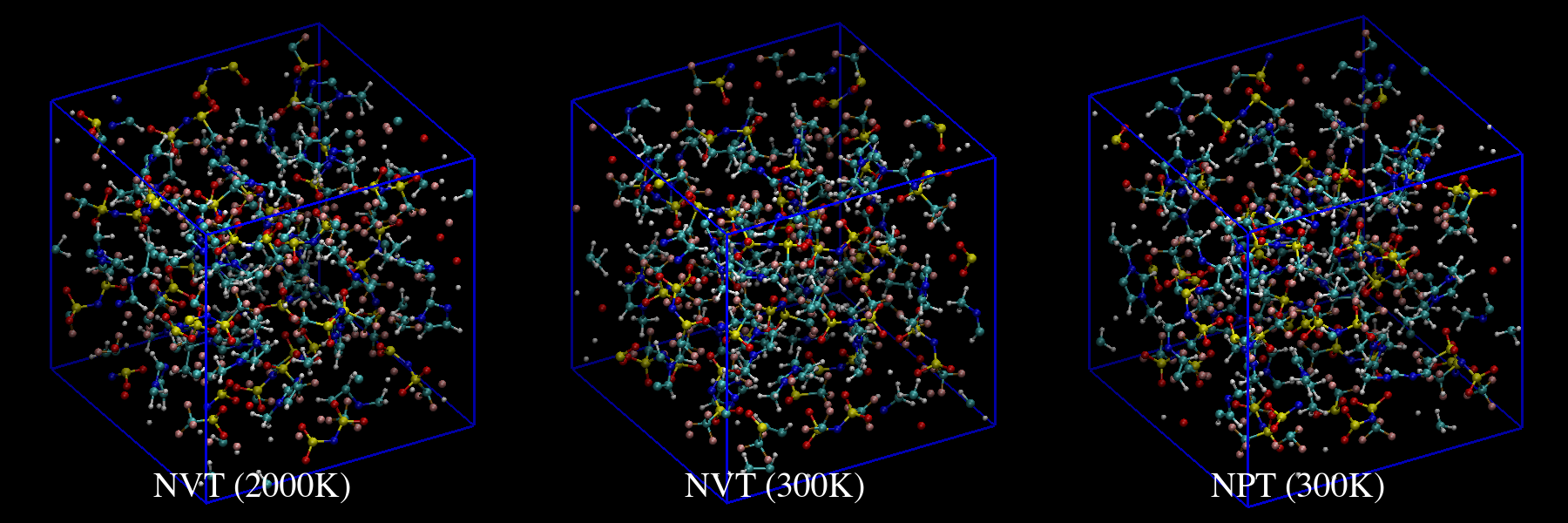
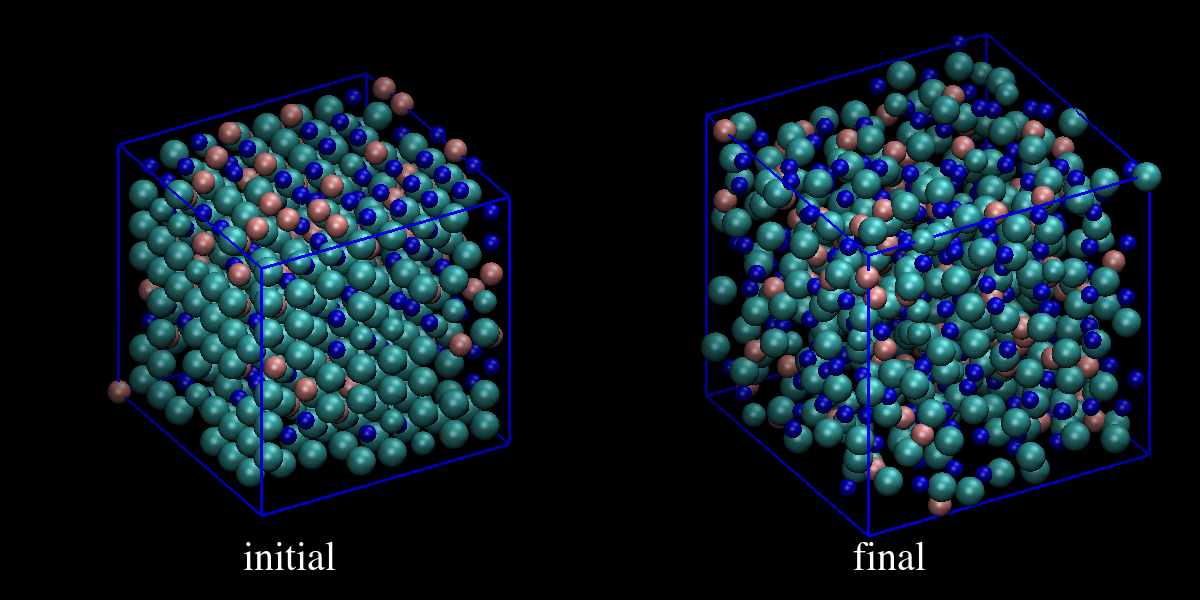
emim-ntf2.dataは、原子が重ならないように大きめの単位胞を初期構造として います。短いステップで平衡構造を得るために2,000 KのNVT計算でアニーリン グし、deformを使って1.5 g/cm3まで体積を減少させならがら300Kまで温度 を下げます。その後、1 atmで300 KのNPT計算を行って平衡構造を得ます。
計算を実行します(Total wall time: 0:01:03)。
mpirun -np 4 lammps -in emim-ntf2.in -log emim-ntf2.log
vmdで可視化して結果を確かめてみます。
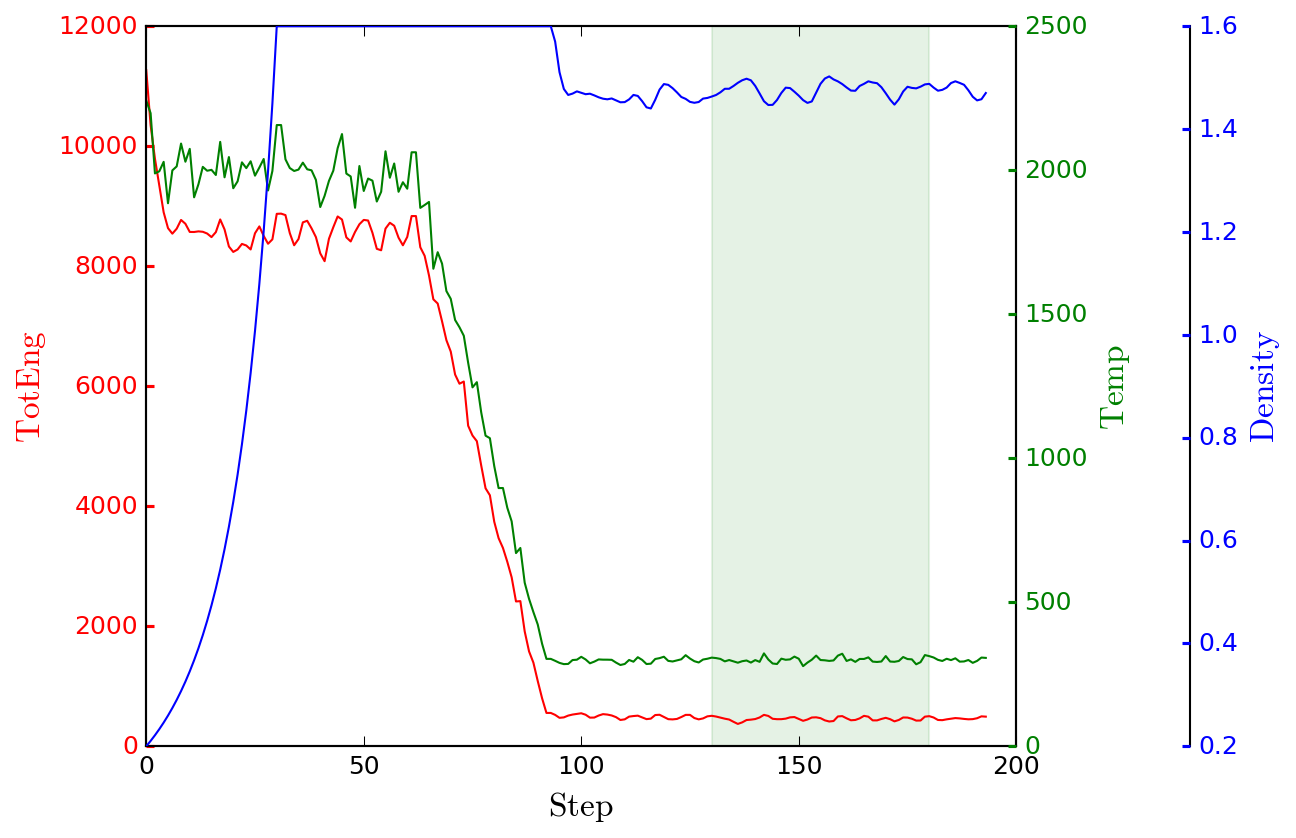
シミュレーションで得られた統計データをプロットします。-wで統計量を評価する範囲を指定します。
logplot.py emim-ntf2.log -k TotEng Temp Density -w 130 180 -o log.png
エネルギーや密度が次のように得られます。
TotEng = 492.565 +/- 27.09 Temp = 297.951 +/- 7.64848 Density = 1.46358 +/- 0.0136792
計算が終了すると最終ステップで得られた平衡構造のemim-ntf2_eq.dataが保存されてます。構造やダイナミクスの評価、粘性計算はemim-ntf2_eq.dataを読んで平衡構造からリスタートすることとします。
構造とダイナミクス評価
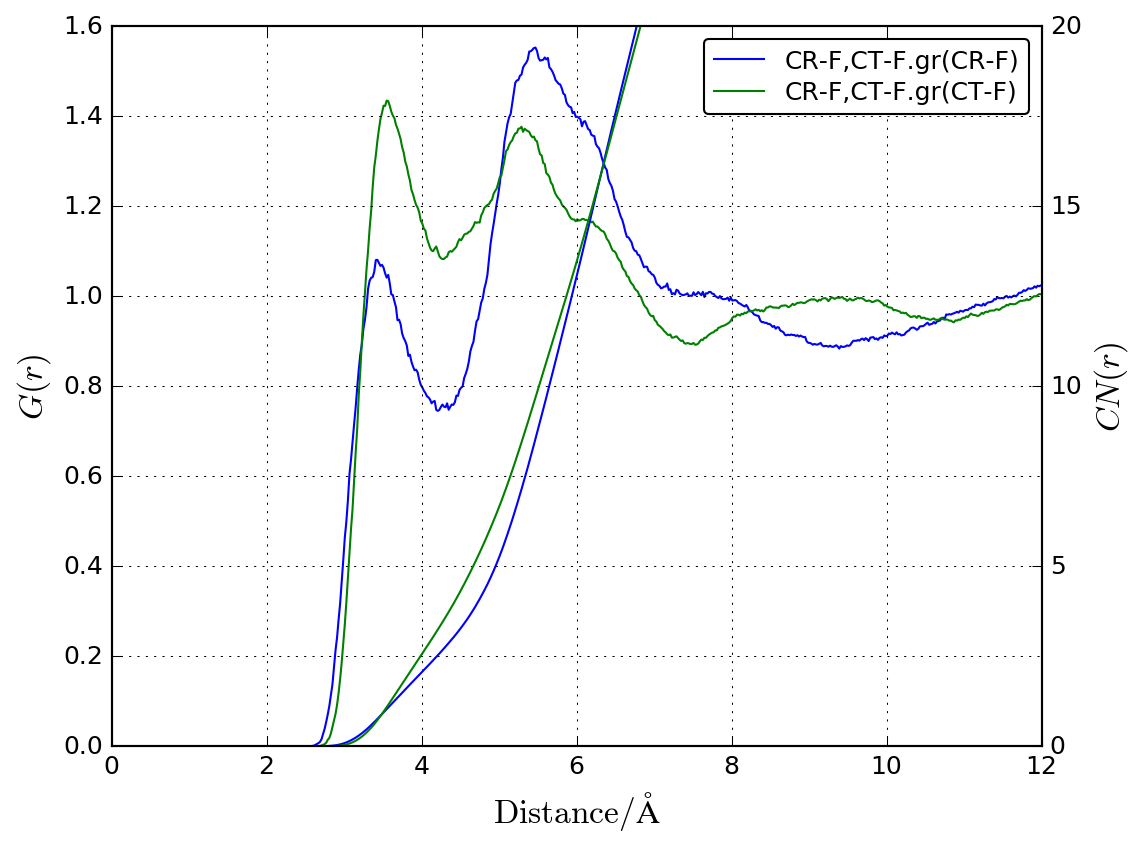
平衡構造からリスタートして次のような動径分布関数と平均二乗変位を計算してみます。
- c2c1imのイミダゾリウム環のCとntf2-のF
- emimのアルキル鎖末端Cとtf2N-のF
- c2c1imのイミダゾリウム環のCの平均自乗変位
- ntf2-のFの平均二乗変位
# Ionic liquid system: [imidazorium][tf2N-], msd and G(r) calculation
units real
atom_style full
pair_style lj/cut/coul/long 12.0 12.0
pair_modify mix geometric tail yes
kspace_style pppm 1.0e-5
special_bonds lj/coul 0.0 0.0 0.5
bond_style harmonic
angle_style harmonic
dihedral_style opls
improper_style cvff
read_data emim-ntf2_eq.data
variable T equal 300
thermo 100
thermo_style custom step temp etotal press vol density
timestep 2.0
group CR type 3 # CR in emim
group CT type 1 # CT in emim
group F type 11 # F in tf2N
# 300 K
compute 1 CR msd
compute 2 F msd
compute 3 all rdf 600 3 11 1 11
fix SHAKE all shake 0.0001 20 0 b 1 5 7
fix 1 all npt temp ${T} ${T} 100 iso 1 1 100
fix 2 all ave/time 1 1 50 c_1[*] &
file CR_${T}K.msd title1 "#dt=2.0fs"
fix 3 all ave/time 1 1 50 c_2[*] &
file F_${T}K.msd title1 "#dt=2.0fs"
fix 4 all ave/time 1 1000 1000 c_3[*] &
file CR-F,CT-F.gr mode vector title1 "#PAIRS=CR-F,CT-F"
run 50000
計算を実行します(Total wall time: 0:03:48)。
mpirun -np 4 lammps -in emim-ntf2-1.in -log emim-ntf2-1.log
動径分布関数をプロットします。計算途中でもプロットできるので、計算ステップが進むに従って統計精度が改善されることを確認できます
grplot.py CR-F,CT-F.gr
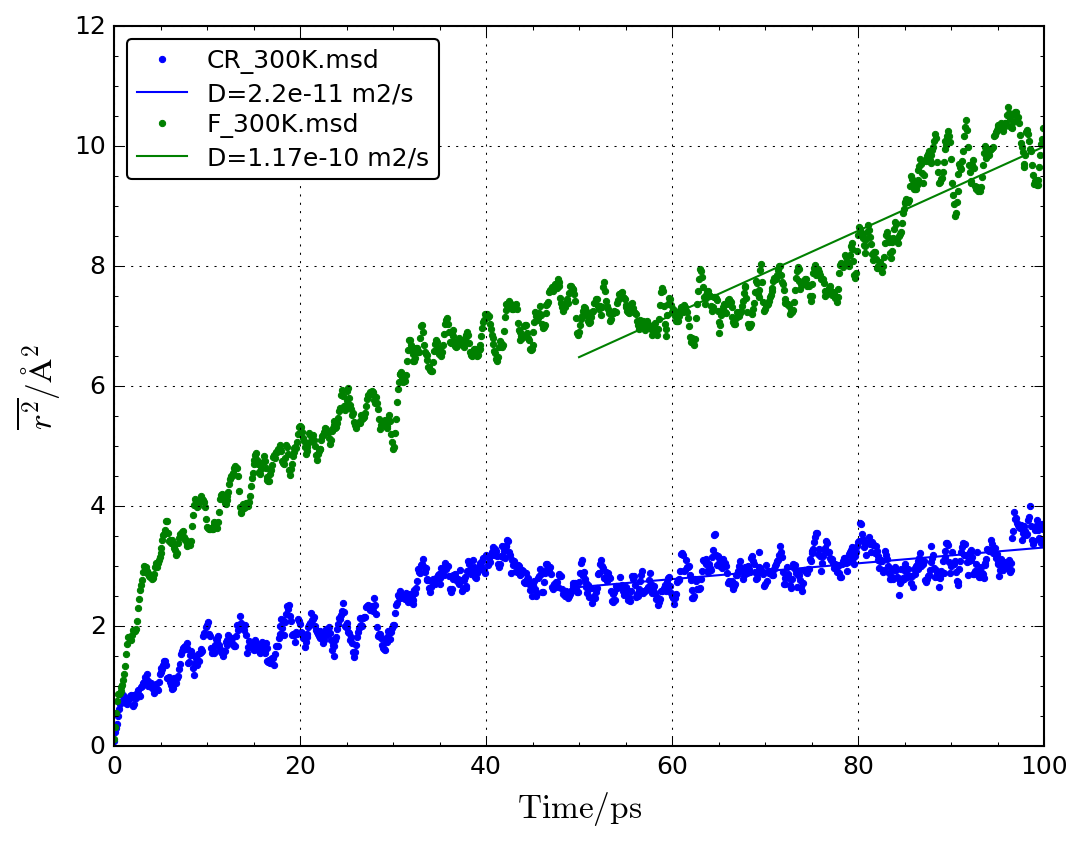
平均自乗変位もプロットして、拡散係数を求めています。50から100 psのデータを使って、直線を求め拡散計算を計算します。
msdplot.py CR_300K.msd F_300K.msd -w 50 100 -o msd.png
統計精度がやや悪いですが、次のように自己拡散計算が得られます。
CR_300K.msd: D=2.58e-11 m2/s F_300K.msd: D=1.03e-10 m2/s
粘性係数の計算
構造とダイナミクス評価と同様に、平衡構造からリスタートして粘性の計算を行います。
# Ionic liquid system: [imidazorium][tf2N-], viscosity calculation
units real
atom_style full
pair_style lj/cut/coul/long 12.0 12.0
pair_modify mix geometric tail yes
kspace_style pppm 1.0e-5
special_bonds lj/coul 0.0 0.0 0.5
bond_style harmonic
angle_style harmonic
dihedral_style opls
improper_style cvff
read_data emim-ntf2_eq.data
variable T equal 300
variable V equal vol
variable dt equal 2
variable DT_ format dt "dt=%.8gfs"
variable T_ format T "T=%.8gK"
variable V_ format V "V=%.8gAng3"
variable title string "#${DT_};${T_};${V_};[Eta_calc.]"
thermo 100
thermo_style custom step temp etotal press vol density
timestep ${dt}
fix SHAKE all shake 0.0001 20 0 b 1 5 7
# to calculate cell size, 300 K NPT run
variable T equal 300
variable xlo_ equal xlo
variable xhi_ equal xhi
variable ylo_ equal ylo
variable yhi_ equal yhi
variable zlo_ equal zlo
variable zhi_ equal zhi
fix 1 all npt temp ${T} ${T} 100 iso 1 1 1000
fix xlo all ave/time 1 50000 50000 v_xlo_
fix xhi all ave/time 1 50000 50000 v_xhi_
fix ylo all ave/time 1 50000 50000 v_ylo_
fix yhi all ave/time 1 50000 50000 v_yhi_
fix zlo all ave/time 1 50000 50000 v_zlo_
fix zhi all ave/time 1 50000 50000 v_zhi_
run 50000
# set equilibrium cell size
unfix 1
variable xlo_ equal f_xlo
variable xhi_ equal f_xhi
variable ylo_ equal f_ylo
variable yhi_ equal f_yhi
variable zlo_ equal f_zlo
variable zhi_ equal f_zhi
fix 1 all deform 1 &
x final ${xlo_} ${xhi_} &
y final ${ylo_} ${yhi_} &
z final ${zlo_} ${zhi_}
unfix xlo
unfix xhi
unfix ylo
unfix yhi
unfix zlo
unfix zhi
fix 2 all nvt temp ${T} ${T} 100
run 50000
# equilibrium under NVT
unfix 1
run 50000
# viscosity calculation for 10 ns
variable pxy equal pxy
variable pxz equal pxz
variable pyz equal pyz
fix 3 all print 1000 "$(step) ${pxy} ${pxz} ${pyz}" &
title ${title} screen no file emim-ntf2.flux
run 50000000
計算を実行します(Total wall time: 45:20:23)。
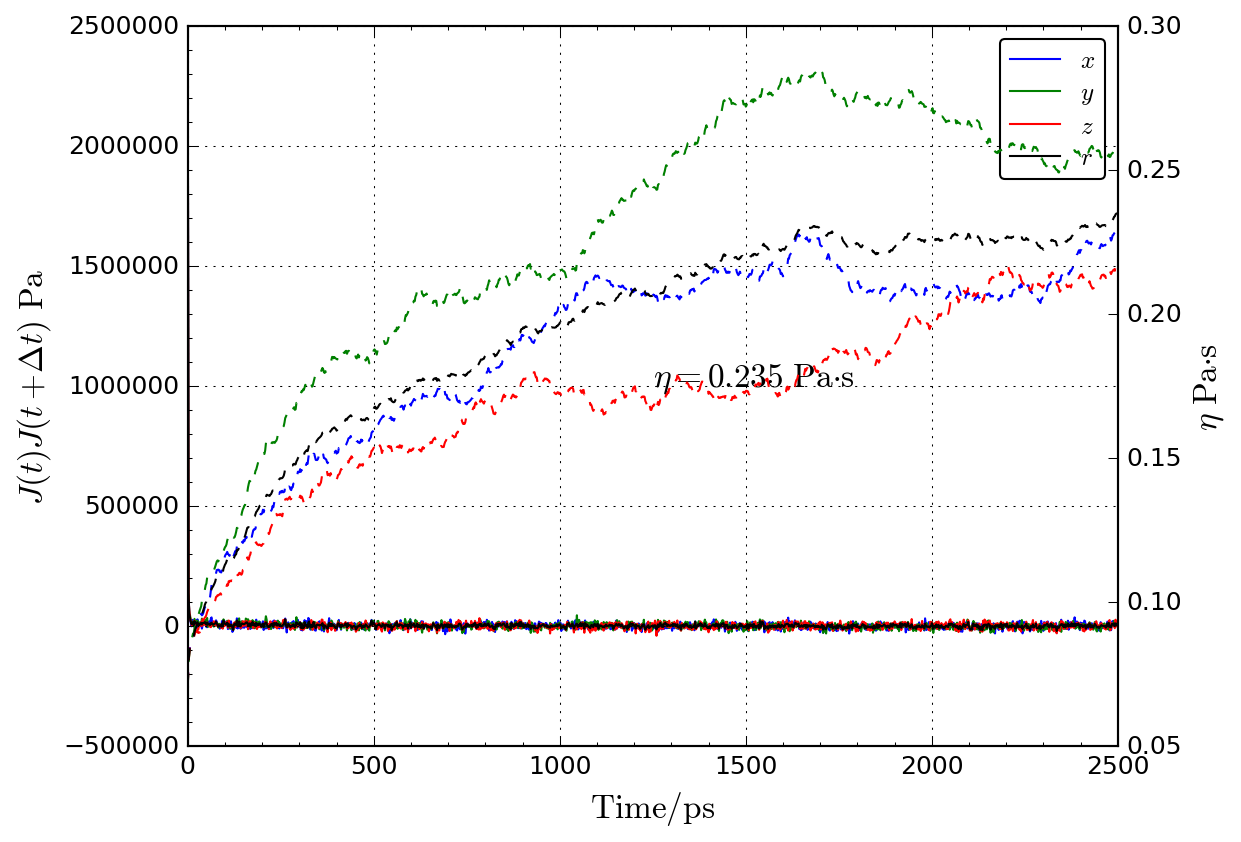
粘性係数を計算するための圧力テンソルがemim-ntf2.fluxに保存されているの で、2.5 nsの時間windowで相関関数を求め積分による粘性係数を計算します。
corrplot.py emim-ntf2.flux -w 2500
少し統計が悪いですが粘性が次のように求まります。
eta = 0.233233 Pa·s eta_xy = 0.280396 Pa·s eta_xz = 0.139562 Pa·s eta_yz = 0.27974 Pa·s
自由課題 (溶融塩, イオン液体, ガラス)
参加者の計算したい組成をもつ溶融塩、イオン液体またはガラスのインプット ファイルを作成し、構造や物性の計算行います。自作スクリプトを使って希望 する系のインプットファイルを作成し計算を行います。
溶融塩の計算
make_ms.pyを適当なアルカリハロゲン溶融塩の組成もつ溶融塩のインプットファ イルを作成し計算を行います。例えば、次の組成をもつ溶融塩のインプットファ イルを作成してみます。-oで生成するインプットファイルのbasenameを指定し ます。
- 100LiCl
- 200NaCl
- 50NaBr
make_ms.py --LiCl 100 --NaCl 200 --NaBr 50 -o 100LiCl-200NaCl-50NaBr
これで700原子からなる溶融塩のインプットファイル (100LiCl-200NaCl-50NaBr.inと100LiCl-200NaCl-50NaBr.data)が生成されます。 初期構造は、アニオンとカチオンのペアをセルの中に等間隔で配置するようし ています。デフォルトの密度は2.0 g/cm3です。
100LiCl-50NaBr-200NaCl: 700 atoms 100LiCl-50NaBr-200NaCl: 0 bonds 100LiCl-50NaBr-200NaCl: 0 angles 100LiCl-50NaBr-200NaCl: 0 dihedrals 100LiCl-50NaBr-200NaCl: 0 impropers initial density: 2.00000 g/cm3 target density: 2.00000 g/cm3 total charge: 0.00000
初期密度や組成を変更したい場合は、引数で指定します。詳細は、-hで表示さ れるヘルプを参照してください。指定できるハロゲン化塩の種類を示します。
| 引数 | 溶融塩 |
|---|---|
| –LiF | Lithium fluoride |
| –LiCl | Lithium chloride |
| –LiBr | Lithium bromide |
| –LiI | Lithium iodide |
| –NaF | Sodium fluoride |
| –NaCl | Sodium chloride |
| –NaBr | Sodium bromide |
| –NaI | Sodium iodide |
| –KF | Potassium fluoride |
| –KCl | Potassium chloride |
| –KBr | Potassium bromide |
| –KI | Potassium iodide |
| –RbF | Rubidium fluoride |
| –RbCl | Rubidium chloride |
| –RbBr | Rubidium bromide |
| –RbI | Rubidium iodide |
| –CsF | Cesium fluoride |
| –CsCl | Cesium chloride |
| –CsBr | Cesium bromide |
total chargeが0になっていることを確認します。作成したインプットファイ ルを編集して、分子動力学計算を実行します。十分にアニーリングした後、平 衡状態になってから動径分布関数や熱伝導率等を計算します。
イオン液体の計算
make_il.pyを使ってインプットファイルを作成し、適当なイオンの組み合わせ からなるイオン液体の計算を行います。例えば、次の組成をもつイオン液体の インプットファイルを作成してみます。-oで生成するインプットファイルの basenameを指定します。
- 20N1111+
- 10c4c4im+
- 13PF6-
- 17ntf2-
make_il.py --N1111 20 --c4c4im 10 --PF6 13 --ntf2 17 -o 20N1111-10c4c4im-13PF6-17ntf2
total chargeが0になっていることを確認します。これで60分子(1026原子)か らなる溶融塩のインプットファイル(20N1111-10c4c4im-13PF6-17ntf2.inと 20N1111-10c4c4im-13PF6-17ntf2.data)が生成されます。初期構造は、密度0.2 g/cm3でイオンをセルの中にランダムに配置するようしています。アニーリ ングしながらdeformで密度1.6 g/cm3までセルを小さくして平衡構造を得る ようなインプットファイルになっています。
初期密度やイオン種を変更したい場合は、引数で指定できます。詳細は、-hで 表示されるヘルプを参照してください。指定できるイオン液体を示します。
| 引数 | イオン液体 |
|---|---|
| –N1110 | 8-(Dibenzo[b,d]thiophen-4-yl)-2-morpholino-4H-chromen-4-one+ |
| –N1111 | tetramethylammonium+ |
| –Na | Na+ |
| –P66614 | trihexyltetradecylphosphonium+ |
| –benzc1im | benzylimidazolium+ |
| –c12c1im | 1-dodecyl-3-methylimidazolium+ |
| –c1c1im | 1,3-dimethylimidazolium+ |
| –c1c1pyrr | N,N-dimethylpyrrolidinium+ |
| –c2OHc1im | 1-(2-hydroxyethyl)3-methylimidazolium+ |
| –c2c1c1im | 1-ethyl-2,3-dimethylimidazolium+ |
| –c2c1im | 1-ethyl-3-methylimidazolium+ |
| –c3c1im | 1-propyl-3-methylimidazolium+ |
| –c3c1pyrr | N-methyl-N-propylpyrrolidinium+ |
| –c4c1c1im | 1-butyl-2,3-dimethylimidazolium+ |
| –c4c1im | 1-butyl-3-methylimidazolium+ |
| –c4c1pyrr | N-butyl-N-methylpyrrolidinium+ |
| –c4c4im | 1,3-dibutylimidazolium+ |
| –c4pyri | N-butyl-pyridinium+ |
| –c6c1im | 1-hexyl-3-methylimidazolium+ |
| –c8c1im | 1-octyl-3-methylimidazolium+ |
| –c8fc1im | 1-(3,3,4,4,5,5,6,6,7,7,8,8,8-tridecafluorooctyl)-3-methylimidazolium+ |
| –gua | guanidinium+ |
| –BF4 | tetrafluoroborate- |
| –Br | Br- |
| –Cl | Cl- |
| –PF6 | hexafluorophosphate- |
| –SCN | thiocyanate- |
| –beti | bis[(pentafluoroethyl)sulfonyl]imide- |
| –c1SO3 | methylsulfonate- |
| –c1SO4 | methylsulfate- |
| –c2SO3 | ethylsulfonate- |
| –c2SO4 | ethylsulfate- |
| –c4fc1fsi | N-(trifluoromethylsulfonyl)-nonafluoroethylsulfonamide- |
| –dca | dicyanamide- |
| –fsi | bis(fluorosulfonyl)imide- |
| –ntf2 | bis(trifluoromethylsulfonyl)imide- |
| –oac | acetate- |
| –otf | methyl triflate- |
| –tfa | trifluoroacetate- |
| –tso | methyl-4-toluenesulfonate- |
作成したインプットファイルで分子動力学計算を実行し、時間ステップ毎のエ ネルギーや密度等を評価して平衡構造が得られることを確認します。場合によっ ては計算ステップ数等を調整して十分にアニーリングし平衡構造を得ます。平 衡状態が得られたら動径分布関数や熱伝導率等を計算してみます。
酸化物ガラスの計算
make_glass.pyを使ってインプットファイルを作成し、適当な酸化物の組み合わせ からなるガラスの計算を行います。例えば、次の組成をもつガラスの インプットファイルを作成してみます。-oで生成するインプットファイルの basenameを指定します。
- 80SiO2
- 50B2O3
- 20Na2O
- 10CaO
make_glass.py --SiO2 80 --B2O3 50 --Na2O 20 --CaO 10 -o 80SiO2-50B2O3-20Na2O-10CaO
これで570原子からなるガラスのインプットファイル (80SiO2-50B2O3-20Na2O-10CaO.inと80SiO2-50B2O3-20Na2O-10CaO.data)が 生成されます。初期構造は、密度2.0 g/cm3で等間隔にセルの中に原子をラ ンダムに配置するようしています。
50B2O3-10CaO-20Na2O-80SiO2: 570 atoms
50B2O3-10CaO-20Na2O-80SiO2: 0 bonds
50B2O3-10CaO-20Na2O-80SiO2: 0 angles
50B2O3-10CaO-20Na2O-80SiO2: 0 dihedrals
50B2O3-10CaO-20Na2O-80SiO2: 0 impropers
initial density: 2.00000 g/cm3
target density: 2.00000 g/cm3
total charge: 0.00000
80: Si
100: B
10: Ca
40: Na
340: O
初期密度やガラスを構成する酸化物を変更したい場合は、引数で指定できます。 詳細は、-hで表示されるヘルプを参照してください。指定できる酸化物を示し ます。
| 引数 | 酸化物 |
|---|---|
| –SiO2 | Silicon dioxide |
| –B2O3 | Boron trioxide |
| –CaO | Calcium oxide |
| –Na2O | Sodium oxide |
| –TiO2 | Titanium dioxide |
| –Al2O3 | Aluminium oxide |
| –Fe2O3 | Iron(III) oxide |
| –FeO | Iron(II) oxide |
| –MgO | Magnesium oxide |
| –K2O | Potassium oxide |
作成したインプットファイルで分子動力学計算を実行し、溶融状態で平衡状態 を得ます。時間ステップ毎のエネルギーや密度等を評価して平衡構造を確認し ます。溶融ガラスの平衡状態が得られたら、冷却して室温にした後、NPTアン サンブルでガラス構造を得ます。
事前講習会
LAMMPSをセットアップして、自前のPCで実行する環境を構築します。またプリ・ ポスト処理でPythonによるプリ・ポスト処理を行うため、Pythonのセットアッ プも行います。エディタは個人の好きなものを選択して良いですが、UNIXの改 行コードでUTF-8でエンコードしたファイルを編集できるものを使ってくださ い。特に何もないようならEmacsをおすすめします(Emacsのlammpsモードを使 えば、インプットファイルが編集しやすいため)。
スケジュール
| 13:00 | 14:00 | Linux, LAMMPS, Python, VMDのセットアップ |
| 14:00 | 15:00 | LAMMPSの実行とVMDによる可視化 |
| 15:00 | 16:00 | UNIXコマンド、簡単なシェルスクリプトの練習 |
| 16:00 | 17:00 | エディタ(Emacs)の使い方等 |
WSL
Debian
Windows storeからDebianを検索してインストールします。
インストールしたら、スタートメニューからDebianを検索してターミナルを 立ち上げます。ターミナルが起動したら右クリックでペーストできるように 簡易編集モードをONにし、umaskを指定しておきます。
echo 'umask 022' >> ~/.profile source ~/.profile
ターミナル上でパッケージをインストールします。まずパッケージシステム をupdateします。パスワードを聞かれるので入力するとupdateがはじまりま す。
sudo apt update
LAMMPSの実行と解析に必要なパッケージをインストールします。パーケージ のダウンロードと展開にしばらくかかります。
sudo apt -y install curl libgl1 libxinerama1 libxi6 openssh-client xkb-data
aptコマンド等のコマンドの使い方は、Debianのパッケージ管理を参照してください。
X-window
Windows用のX-windowとしてVcXsrvをインストールします。
https://sourceforge.net/projects/vcxsrv/
インストーラーをダウンロードしたら実行して指示に従えばインストールが 完了します。デスクトップにXLaunchのショットカットが生成するのでダブル クリックしてX-windowを起動します。VcXsrvを起動すると右下にXのアイコン が表示さます。MacOSはX-windowをインストールする必要はありません。
実行ファイル一式の配布
コンパイル済の実行ファイルとPython環境一式をdownloadして$HOMEに展開し ます(学内からのみアクセスできます)。ファイルの書き込みがネックになっ て、5分くらいかかります。
- Windows+WSL(Linux用):
curl https://amorphous.tf.chiba-u.jp/lecture.files/ms-workshop/dist/linux/linux_package.tgz | tar xzf - -C ~/
Windows+WSLの人はmpirunを実行するとエラーが表示されるのでおまじないを唱える。
echo 0 | sudo tee /proc/sys/kernel/yama/ptrace_scope
dotファイルをインストールします。.bashrcを上書きするので、 自前のファイルがある場合は退避させて自分でmergeしてください。
curl https://amorphous.tf.chiba-u.jp/lecture.files/ms-workshop/dist/linux/bashrc.tgz | tar xzf - -C ~/ source ~/.bashrc
- MacOS用:
curl https://amorphous.tf.chiba-u.jp/lecture.files/ms-workshop/dist/macos/macos_package.tgz | tar xzf - -C ~/
dotファイルをインストールします。.bashrcを上書きするので、 自前のファイルがある場合は退避させて自分でmergeしてください。
curl https://amorphous.tf.chiba-u.jp/lecture.files/ms-workshop/dist/macos/bashrc.tgz | tar xzf - -C ~/ source ~/.bashrc
- Pythonスクリプトのみ
自前でPython環境を構築している場合は、Pythonスクリプトのみを展開して ください。$HOME/pyに展開しますので、適当にパスを通してください。
curl https://amorphous.tf.chiba-u.jp/lecture.files/ms-workshop/dist/py.tgz | tar xzf - -C ~/
実行テスト
上手くインストールできているか確認するために、LAMMPSを実行してみます。 インプットファイルをダウンロードして2コアで並列計算してみます。
curl https://amorphous.tf.chiba-u.jp/lecture.files/ms-workshop/dist/data.tgz | tar xzf - -C ~/ cd data/example mpirun -np 2 lammps -in NaCl.in
計算結果が表示されれば、インストールは完了しています。LAMMPSが実行で きると画面に計算経過が表示されます。
mpirunで指定する計算機のコア数等の計算資源はtask managerで確かめるこ とができます。また、計算が完了したらログファイルをプロットします。 LinuxではX-windowが起動していなとプロット画面が表示されません。
logplot.py log.lammps
プロットした結果が表示されれば問題なく全てインストールされています。 libGLでターミナルにエラーが 出る場合は、VcXsrvの起動時にNative opengl を外してX-windowを起動します。
さらにvmdで可視化してみます。うまく実行されると計算結果が可視化できます。
vmd NaCl.lammpstrj
VMD
計算結果を可視化するためにVMDをインストールします。以下のURLに接続し てOSにあったファイルをダウンロードします。最初にダウンロードする時に、 Usernameの登録が求められるので指示に従います。 https://www.ks.uiuc.edu/Research/vmd/
Python
自前でPython3.7をインストールする場合は、以下のモジュールが必要です。 miniconda等を使ってインストールします。
- numpy
- matplotlib
VESTA
結晶構造の共通フォーマットであるCIFファイルを可視化したり対称性を操作 するためにVESTAをインストールします。 https://jp-minerals.org/vesta/jp/
Emacs
インプットファイルの編集用にemacsエディタと日本語入力用のmozcをインス トールします。emacsを使わないのであれば、emacsのインストールは必要あ りません。インストールにかなり時間がかかります。
- Windows+WSL:
sudo apt -y install emacs emacs-mozc fonts-noto-cjk
- MacOS:
パッケージをダウンロードしてインストールします。 https://emacsformacosx.com/
- 初期化ファイルのインストール
MacOSとLinuxで共通です。
curl https://amorphous.tf.chiba-u.jp/lecture.files/ms-workshop/dist/emacs.d.tgz | tar xzf - -C ~/
Debianの日本語化
日本語表示になるようロケールを設定する。
sudo dpkg-reconfigure locales
メニューに入ったらja_JP.UTF-8を選択する。環境変数をセットしておく。
echo 'export LC_ALL=ja_JP.UTF-8' >> ~/.bashrc source ~/.bashrc
その他
計算時間
LAMMPSのインストール
aptの利用
packageで準備されているので簡単にインストールできます。
apt install lammps
手動コンパイル
標準でインストールされていない機能を使いたい、LAMMPSを改造して使いた いというときは、Lammpsのソースコードを取得して自前でコンパルする必要が あります。
LAMMPSのコンパルとリンクに必要なコンパイラ(g++)はaptを利用します。フー リエ変換用のfftw3と並列計算用のopenmpi、lammpsのソースコードを取得します。
git clobe https://github.com/FFTW/fftw3.git git clone https://github.com/open-mpi/ompi.git git clone -b stable https://github.com/lammps/lammps.git lammps
コンパイラの環境変数を設定します。intel製のコンパイラやMKLライブラリを 購入している人は、そちらでコンパイル・リンクした方が早いです。コンパイ ラやオプションの環境変数をセットしておきます。
export CC=gcc export CFLAGS=-O3 export CXX=g++ export CXXFLAGS=-O3 export FC= gfortran export F77=gfortran export FFLAGS=-O3 export FCFLAGS=-O3
fftwをconfigureしてmakeします。
cd fftw ./configure make -j4 sudo make install
openmpiをconfigureしてmakeします。
cd openmpi ./configure make -j4 sudo make install
PCをまたいだ複数のノード(分散メモリ)で計算した場合は、各ノードにmpiを導入する必 要があります。自作したい場合は、研究室で構築した並列計算機のメモが少し は役に立つかもしれません。
lammpsをコンパイルします。srcディレクトリに移動して必要な拡張機能のソースコードを追加します。
cd lammps/src make yes-RIGID make yes-KSPACE make yes-MOLECULE
MAKE以下にあるコンパイル用のMakefileを編集します。ewald法等の 長距離クーロン相互作用を計算するために、フーリエ変換ライブラリ(fftw3) を利用するので、ライブラリの場所をMakefile中で指定します。
mpiを使わない場合は、dummy用のライブラリを作っておく必要があります。 STUBSに移動してライブラリを作成する必要があります。
MAKE/Makefile.mpiを適当な名前にコピーします。
cp MAKE/Makefile.mpi MAKE/Makefile.hoge
コピーしたらMakefile.hogeを編集して自分の環境にあわせます。コンパイルします。
make hoge -j4
Makefile.hogeならばlmp_hogeの実行ファイルが生成されます。
本講習会について
本講習会は電気化学会溶融塩委員会の主催で開催されます。 http://msc.electrochem.jp/index.html