大学院 無機材料化学
目次
- お知らせ
- ガイダンス
- 講義: 計算科学と工学
- 講義: 分子動力学計算の理論
- 講義: 液体Arの分子動力学計算
- 実習: lammpsとVMDのセットアップ
- 実習: 液体Arの分子動力学計算
- 講義: NaClの分子動力学計算
- 講義資料
- 参考論文
- Dispersion and Polarizability and the van der Waals Potential in the Alkali Halides.pdf
- Interatomic Distances in Crystals of the Alkali Halides.pdf
- Ionic sizes and born repulsive parameters in the NaCl-type alkali halides—I.pdf
- Ionic sizes and born repulsive parameters in the NaCl-type alkali halides—II.pdf
- Calculation of the melting point of NaCl by molecular simulation.pdf
- 実習: NaClの分子動力学計算
- 講義: 鉱物の分子動力学計算
- 実習: 鉱物の分子動力学計算
- 講義: 平面波第一原理計算の理論
- 実習: QEとVESTAのインストール
- 実習: Siのscf計算
- 実習: Siの構造最適化計算
- 実習: バンド計算
- その他
お知らせ
課題の提出と採点はGoogle Classroom上で行います。 クイズはGoogle Classroom上でのオンライン提出となります。以下のURLにアクセスしてGoogle Classroomに参加してください。
https://classroom.google.com/c/NzY3MjI0MDAyNjEy?cjc=cwlmg4gb
ガイダンス
無機材料の構造や物性予測で用いられる分子シミュレーションの理論と技法を講義します。シミュレーションを通じて結晶学の基本的なこと、無機材料の原子・電子構造と特徴、ダイナミクスの理解を目指します。講義の半分は座学とし、残りの半分はPCを持参してもらって各自でシミュレーションを行なって理解を深める。適時、課題を与えるので自前のPCでシミュレーションを実行しレポートと計算コードを作成して提出してもらいます。
講義予定
最初に講義の意義を説明します。次に分子動力学計算の理論・実践を行います。 最後に平面波基底の第一原理計算の理論・実践を行います。
成績評価について
授業への参加度合いとレポートの内容で評価します。
講義: 計算科学と工学
- ガイダンス資料.pdf
- 計算科学について
- 工学分野の平均給与と今後の予測
- 評点について
- 計算のためのPC環境の構築
講義: 液体Arの分子動力学計算
論文 Correlations in the Motion of Atoms in Liquid Argon.pdf
- Author: A. Rahman (Argoone National Lab.)
- Physical Review A, 136, 405-411 (1964)
- Abstruct: A system of 864 particles interacting with a I.ennard-Jones potential and obeying classical equations of motion has been studied on a digital computer (CDC 3600) to simulate molecular dynamics in liquid argon at 94.4 K and a density of 1.374 g/cm3. The pair-correlation function and the constant of self-di6usion are found to agree well with experiment; the latter is 15%lower than the experimental value. The spectrum of the velocity autocorrelation function shows a broad maximum in the frequency region of the Van Hove function G,(r,t) attains a maximum departure from a Gaussian at about s=3 X10 "sec and becomes a Gaussian again at about 10 "sec. The Van Hove function G(r, t) has been compared with the convolution approximation of Vineyard, showing that this approximation gives a too rapid decay of Gd, (r,t) with time. A delayed-convolution approximation has been suggested which gives a better 6t with Gz(r, I); this delayed convolution makes Gz(r, t} decay as t4 at short times and as I at long times.
- 回折実験の基本 scatter_theory.pdf
- 原子散乱因子 International Tables for Crystallography (2006). Vol. C, Chapter 6.1, pp. 554–595.)の表 structural factor.pdf
- f(q)の近似式は P. 565のEq.6.1.1.15を使う
- f(q)の近似式のテーブルは P.578あたり
- 一例としてHからNeのf(q) scattering-factor.pdf
実習: lammpsとVMDのセットアップ
Windows
lammpsはUSのSandia National Laboratoryで無料で配布されている汎用分子 動力学計算プログラムです。Lammpsの実行ファイルを入手してをコマンドラ インから計算方法を記述したインプッファイルを指定することで、MD計算を 行うことができます。MD計算のための環境を整えるのがやや面倒なので、簡 単に実行できるよう実行環境を大窪が作成しています。以下の手順に従って 計算環境を作ります。
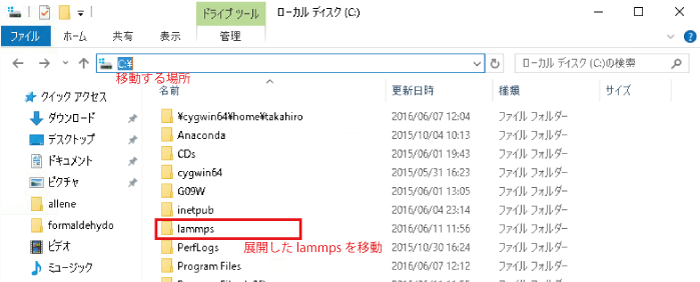
- lammpsのwindows用バイナリファイル(lammps_win32.zip)をダウンロードして展開する。
展開したlammpsを「C:」に移動する。
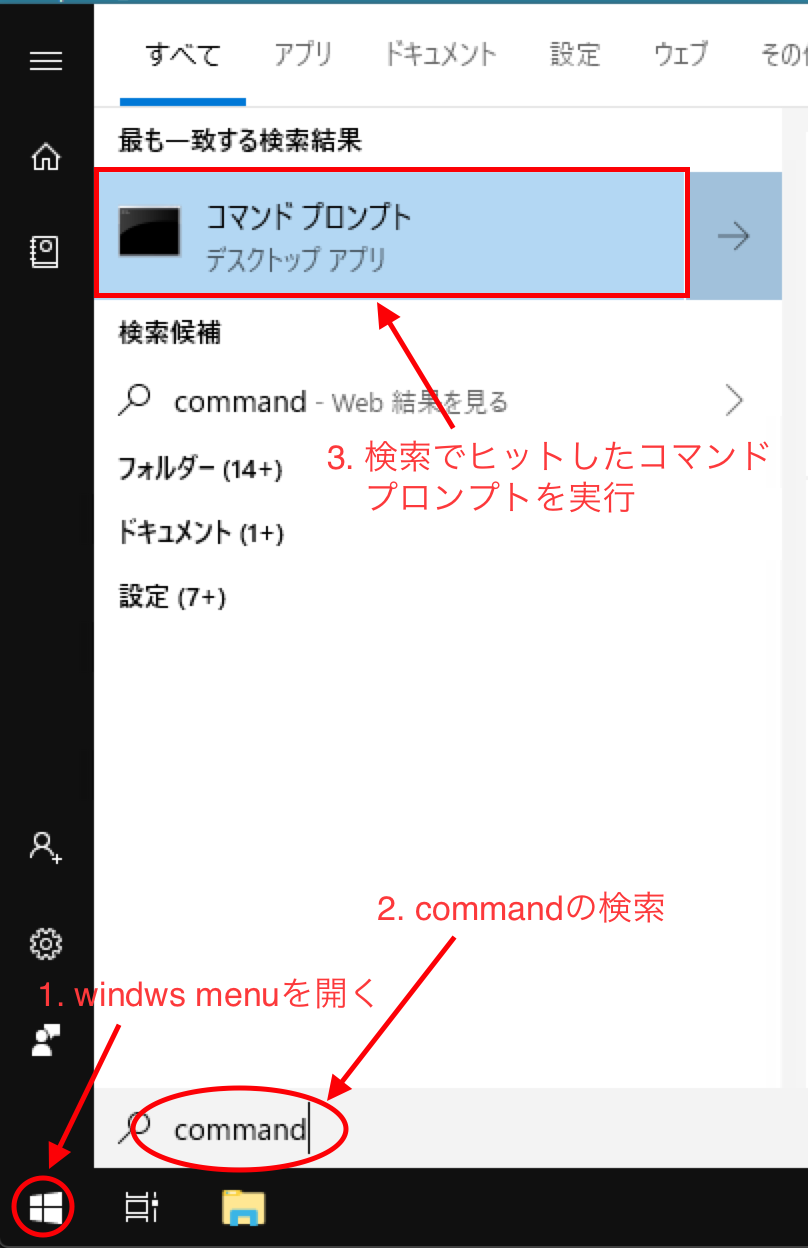
windowsのスタートメニューを開いて「command」を検索しコマンドプロンプトを実行します。
以後全てコマンドプロンプト上でコマンドラインにて作業を行います。 最低限、次のコマンドを覚えておけば大丈夫です。(矢印の↑でコマンドの履歴を呼び出せます)
cd folder_name folder_nameに移動 cd .. 1つ上のフォルダに移動 dir folderに存在するファイル一覧を表示 (macの人はdirの代わりにls) Ctrl-c Ctrl-cで実行中のプログラムを強制終了
cdコマンドを使って「C:¥lammps」まで移動します。移動したら次のコマ ンドを入力してlammpsが正しく実行されるか確認します。
lammps -in sample.in
コマンドを入力した後に、次のように画面にずらずらと出力結果が表示さ れたら、コマンドは正しく実行されています。
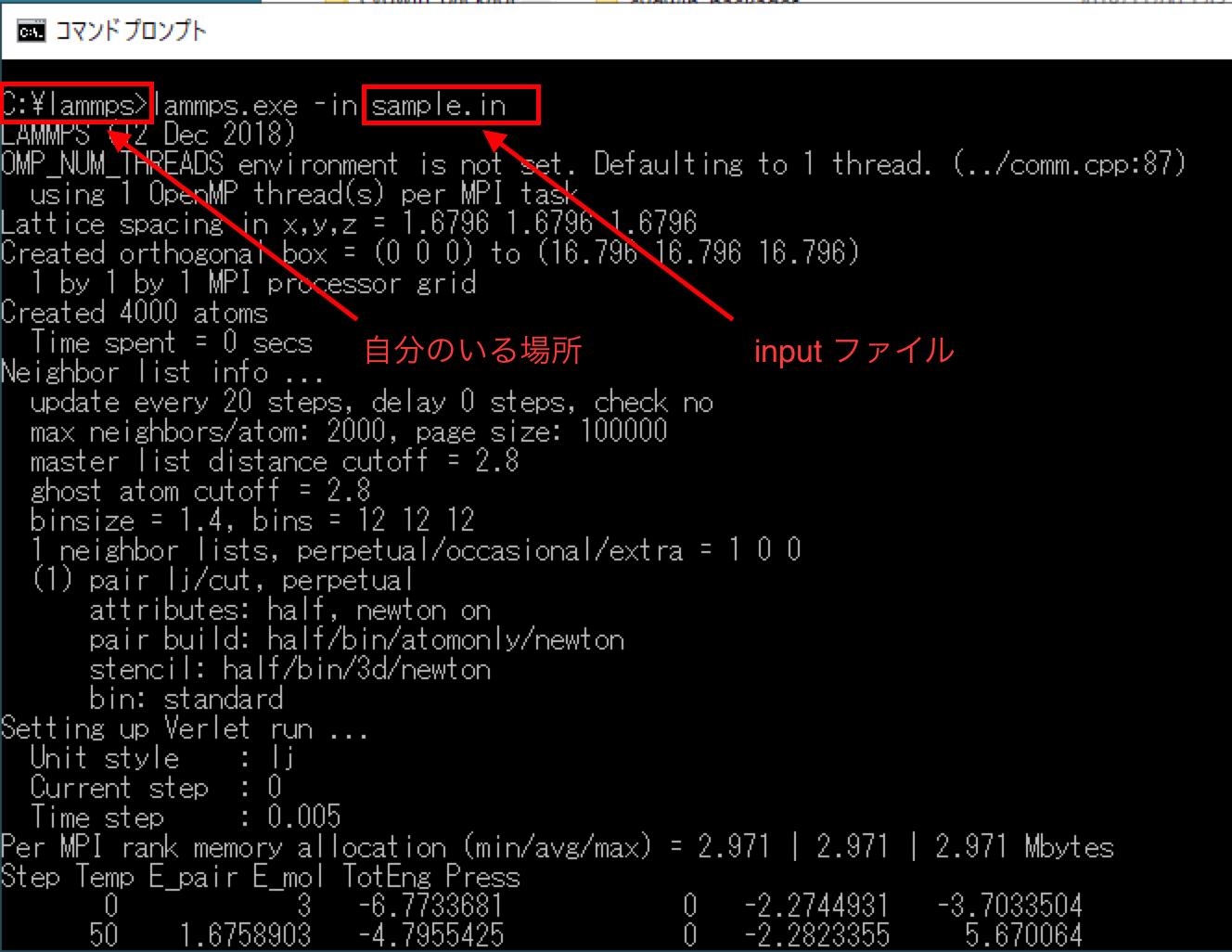
細かい数字は上の出力結果と異なっていても問題ないです。
Mac OSX
- macの人はlammps_osx.tgzをダウンロードしてデスクトップに配置します。ターミナルを開いてDesktopに移動してからtarで展開してください。
# cd Desktop # tar xvzf lamps_osx.tgz
- 後はターミナルで操作できます。lammpsを展開したディレクトリに移動して以下のコマンドを実行しwindowsと同じような出力が得られた正しく実行されています。実行ファイルのパスを示す「./」を忘れないようしてください。
cd lammps (lammpsフォルダに移動) ./lammps -in sammple -in (lammpsの実行)
Linux
少なくとも最新のDebianでは、lammpsがpackage化されていて、aptで簡単に インストールできます。
sudo apt install lammps
これで、並列計算環境のopenmpiを含む一式がインストールされます。
VMDのインストール
lammpsから得られた計算結果を可視化するプログラムです。無料配布していますので、自分のOSに合ったファイルを各自ダウンロードして展開してください。展開して生成されるフォルダの中に入っているvmd.exeが実行ファイルです。VMDの配置場所はどこでも良いですが、日本語のパスが入らないところに配置してください。
- windows用: vmd_win32.zip
- mac osx用(10.14以前): vmd_osx.zip
- mac osx用(10.15以降): vmd_osx10.15.zip
実習: 液体Arの分子動力学計算
インプットファイル
- 密度は1.374 g/cm3(論文と同じ)とします。入力ファイルをAr_lammps.zipをダウンロードして展開後に得られるAr.inとAr.dataをlammpsフォルダに配置します。
- インプットファイル(Ar.inとAr.data)の中身を理解します。インプットファイルの解説: Ar_in_data.pdf
- lammpsを実行します。-inでインプットファイル、-logで出力の保存ファイルを指定します。
- 標準出力にエネルギーや温度等の系の情報が出力されます(Ar.logに同じ内容が保存されている)。Ar.inを編集して温度や計算時間等を変えてMD計算を実行します。
課題: Arの沸点予測(問2まで最低限行うこと)
課題はすべて8x8x8のセル(512原子)のArで2.5fsの時間ステップのNPT計算と する。
- 70Kから10K刻みに140Kまで温度を変えて計算を 行い、平衡に達する時間以降の体積を使って密度を求める(平衡に達する 時間は自分で求めること)。温度と密度(体積から計算)の結果をプロット して相転移の起こる温度範囲を求める。(110K付近になり実測値83Kと異 なるが融点のような相転移は計算で予測することが難しい問題の1つです) 答え: energy-density.png, temperature-density.png
- 液体領域での温度変化(\(\Delta T\))に対するエネルギー変化(\(\Delta E\))から以下の式により定圧モル比熱(\(C_p\))を計算する。\[ C_p = \frac{\Delta E}{\Delta T} \] ※エンタルピー 変化は\(\Delta H = \Delta E\) としています。 答え: Cp.png
- 100Kから600Kまで100K刻みで得られる1ステップ分の原子の速度から速度 分布を求め、Maxwell-Boltzmann速度分布式と一致するか確かめる(余裕 のある人向けの追加課題)。velocity.png
締切: 5月27日(月)10:00までに大窪(ohkubo.takahiro@faculty.chiba-u.jp)までemailにpdfファイルを添付して提出してください。メールの題名(Subject:)は以下のフォーマットを守ってください。添付ファイルのファイル名は自由ですがpdfファイルとしてください。
無機材料化学第1回レポート 19WM7777 山田純一
スペース、英数字はすべて半角文字としてください。ファイルは必ずpdfにし て送ってください。
講義: NaClの分子動力学計算
参考論文
Interatomic Distances in Crystals of the Alkali Halides.pdf
- Author: M.L. Huggins and J.E. Mayer
- J. Chem. Phys., 1, 643-646 (1933)
- The constants of the empirical repulsion potential assumed by Born and Mayer between two ions, which may be termed the ionic "radii," are calculated for the alkali and halide ions from the lattice constants of the alkali halides. By using 9 such radii the 20 lattice constants can be recalculated nearly within the probable experimental error of their determination. The good agreement is regarded as support for the assumptions involved in the calculations.
Ionic sizes and born repulsive parameters in the NaCl-type alkali halides—I.pdf
- Author: F. G. Fumi and M. P. Tosi
- J. Phye. Chem. Solids, 25, 31-43 (1964)
- Abstruct: The Born model of ionic solids is shown to permit the complete determination from solid-state data of crystal radii for the alkali and halogen ions in the individual alkali halides with the NaCl structure, which are directly comparable with the experimental crystal radii deducible from the X-ray maps for the electron distribution in the crystal.
Ionic sizes and born repulsive parameters in the NaCl-type alkali halides—II.pdf
- Author: F. G. Fumi and M. P. Tosi
- J. Phys. Chem. Solids, 25, 45-62 (1964)
- Abstruct: procedure described in I for the determination of the crystal radii of the ions in the individual NaCl-type alkali halides from solid-state data by the Born model is applied, adopting a generalized Huggins-Mayer form for the Born repulsive energy (i.e. allowing the hardness para- meter to vary from salt to salt).
Calculation of the melting point of NaCl by molecular simulation.pdf
- Author: J Anwar and D. Frenkel
- J. Chem. Phys., 118, 728-735 (2003)
- Abstruct: We report a numerical calculation of the melting point of NaCl. The solid–liquid transition was located by determining the point where the chemical potentials of the solid and liquid phases intersect.
実習: NaClの分子動力学計算
インプットファイル
- 入力ファイル: NaCl_lammps.zip
- NaCl.inを読んで中身を理解する。NaCl.in.pdf
- 提出期限: 7/19の講義開始前
課題: NaCl固体および融体の構造と動的挙動の計算
固体と液体状態のNPT計算を行い以下の解析(図1から図5を作成)を行う。解析結果について考察していると、加点します。
- 300Kと1500Kの構造から、各温度でのNa-Clの動径分布関数を計算する(図1)。第一ピークからNa-Cl距離を求める。
- 300Kと1500Kの構造から、各温度でのNaまわりのClの配位数を距離の関数として計算する(図2)。動径分布関数の第一ピークが最小になる距離からNaに配位したClの数を求める。
- 300KでNaとClの平均二乗変位(MSD)を計算し温度因子を計算する(図3)。
- 1600K, 1800K, 2000K, 2200K, 2400KでのNaのMSDを計算しプロットする。プロットの直線領域から拡散係数を計算する(図4)。
- 拡散係数の温度依存性から拡散の活性化エネルギーを計算する(図5)。
余裕のある人向け課題: NaClと同様にLiClとCsClについても動径分布関数を計算
LiCとCsClのポテンシャルは以下のとおりです(Handbook of interatomic potentials より)。 \[ U_{ij} = A_{ij}\exp\left(-\frac{r}{\rho}\right) - \frac{C_{ij}}{r^6} - \frac{D_{ij}}{r^8} + \frac{q_iq_j}{r} \] ポテンシャル関数のパラメータ(\(A_{ij}, \rho, C_{ij}, D_{ij}\))は以下のとおりです。カットオフ距離はNaClと同じで良いです。
| pair | \(A_{ij}\) /eV | \(\rho\) /Å | \(C_{ij}\) /eVÅ6 | \(D_{ij}\) /eVÅ8 |
|---|---|---|---|---|
| Li-Li | 0.4919 x 109 | 0.0260 | 0.06 | 0.02 |
| Li-Cl | 0.2451 x 105 | 0.2000 | 2.71 | 2.41 |
| Cl-Cl | 0.3361 x 104 | 0.3564 | 193.92 | 269.12 |
| Cs-Cs | 8908 | 0.3234 | 411 | 751.0 |
| Cs-Cl | 5602 | 0.3234 | 0 | 0 |
| Cs-Cs | 3523 | 0.3234 | 349 | 702.5 |
- \(\sigma\) を0として関数系を born/coul/long に合わせる。
- 単位変換に注意 答え: CsCl-LiCl_gr.png (Csの配位数は6, Liの配位数は12です)
締切: 6月17日(月)10:00までに大窪(ohkubo.takahiro@faculty.chiba-u.jp)までemailにpdfファイルを添付して提出してください。メールの題名(Subject:)は以下のフォーマットを守ってください。添付ファイルのファイル名は自由ですがpdfファイルとしてください。
無機材料化学第2回レポート 19WM7777 山田純一
スペース、英数字はすべて半角文字としてください。ファイルは必ずpdfにして送ってください。
講義: 鉱物の分子動力学計算
参考論文
- 論文 Molecular Models of Hydroxide, Oxyhydroxide, and Clay Phases and the Development of a General Force Field.pdf
- clayFFを利用したMD計算の例
- Large-Scale Molecular Dynamics Study of Montmorillonite Clay- Emergence of Undulatory Fluctuations and Determination of Material Properties.pdf
- Simulations of the Quartz(1011):Water Interface- A Comparison of Classical Force Fields, Ab Initio Molecular Dynamics, and X-ray Reflectivity Experiments.pdf
- Molecular Dynamics Simulations of Water Structure and Diffusion in Silica Nanopores.pdf
- Structural Arrangements of Isomorphic Substitutions in Smectites- Molecular Simulation of the Swelling Properties, Interlayer Structure, and Dynamics of Hydrated Cs−Montmorillonite Revisited with New Clay Models.pdf
実習: QEとVESTAのインストール
Quantum Espressoはフリーでソースコードが配布されている平面波第一原理計 算用プログラムです。 インストールがややこしいのでwindows用とmac用に作 成したものを以下のURLからダウンロードして展開してください。
- windows用プログラム qe_win.zip
- mac用プログラム qe_mac.tar
VESTA
VESTAは結晶構造や電子密度等を可視化できるフリーのプログラムです。以
下のURLから自分のOSに合ったものをダウンロードしてインストールしてく
ださい。
https://jp-minerals.org/vesta/jp/
実習: Siのscf計算
Siのscf計算するためのインプットファイル(Si_in.pdf)を読んで中身を理解 し、Siのcifファイル(Si.cif)とインプットファイルの中身を比べて内容を確 認します。
プログラムの実行は、qeフォルダに移動して以下のコマンドを実行します。
pw.x < Si.in > Si.log
画面になにも表示されませんが、Si.logに結果が入っています。 Si.logファイルから特定の文字列を含む行を表示させたい場合は、findコマンドを使います。
find "energy" Si.log
macの場合はqeに移動した後、以下のようにおまじないを唱えます。
export DYLD_LIBRARY_PATH=$PWD:$DYLD_LIBRARY_PATH
一度、おまじないを唱えれば、以下のコマンドで実行できます。
./pw.x < Si.in > Si.log
Si.logファイルから特定の文字列を含む行を表示させたい場合は、findでなくgrepです。
grep "energy" Si.log
収束チェック
計算で得られる全energyが、k点の数とcutoff energyで収束していること を確認します。k点の数と平面波のcutoff energy(ecutwfc)を増やせば、一 般的に全energyがどんどん小さくなりますが、その変化が10-3 Ry/atom以 下になる条件を探します。k-meshは、格子定数(a, b, c)と以下のような関係 を目安にします。求めたい物理量や精度などで変わりますのであくまで目安 です。ceilは少数点繰り上げの意味です。
\[ Nx = {\rm ceil}\left(5*\frac{2\pi}{a}\right)\\ Ny = {\rm ceil}\left(5*\frac{2\pi}{b}\right)\\ Nz = {\rm ceil}\left(5*\frac{2\pi}{c}\right)\\ \]
Siの電子密度計算
全エネルギーが収束する条件でscf計算を完了したら電子密度を計算します。電子密度を計算するためのインプットファイル (Si_pp.pdf)を読んで中身を理解します。
pp.x < Si.pp
うまく計算が終わるとSi.xsfが生成されるのでVMDやvestaで表示します。
課題: SCFサイクルの確認
- ecutwfc=60 Ry、 k-mesh=6 6 6で計算を行い各SCFサイクルでのエネルギー 変化をlogファイルから抜き出してプロットする。プロットした結果が収 束条件 conv_thr=1e-6を満たしてSCFサイクルが終了していることを確認 する。
- ecutwfcを20Ryから10Ryずつ増やしながら計算を行い、エネルギーの精度が10-4 Ry/atomを満たす条件を求める。
- 2で求めたecutwfcで、k点を少し増やして計算を行いエネルギーの精度が10-4 Ry/atomを満たしていることを確認する。
- pp.xを使ってSi-diamond.xsfファイルを作成し、可視化する。
締切: 7月8日(月)10:00までに大窪(ohkubo.takahiro@faculty.chiba-u.jp)までemailにpdfファイルを添付して提出してください。メールの題名(Subject:)は以下のフォーマットを守ってください。添付ファイルのファイル名は自由ですがpdfファイルとしてください。
無機材料化学第3回レポート 19WM7777 山田純一
スペース、英数字はすべて半角文字としてください。ファイルは必ずpdfにして送ってください。
実習: Siの構造最適化計算
SCFで求めた波動関数に基づいて、力を計算し構造最適化を行います。
Si-diamond.inのcalculationを次のように変更します。
calculation = 'relax'
さらにelectronsカードの下に構造最適化のためのrelaxカードを追加します。
&ions ion_dynamics = 'bfgs' ! ['bfgs'] /
格子定数も最適化する場合、calculationを次のように変更します。
calculation = 'vc-relax'
さらにionsカードの下に格子定数最適化のためのcellカードを追加します。 cell_dofreeで最適化したい格子定数の条件を指定できます。
&cell cell_dynamics = 'bfgs' ! ['bfgs'] cell_dofree = 'all' ! [all] /
立方晶でFのSiのvc-relax計算すると、格子ベクトルは次のようになります。
CELL_PARAMETERS (alat= 10.30184201) a(1) = ( -0.501700 -0.000000 0.501700 ) a(2) = ( 0.000000 0.501700 0.501700 ) a(3) = ( -0.501700 0.501700 -0.000000 )
これは、立方晶のFが三方晶のRに変換されたためです。a(1)とa(2)の角度を計 算すれば納得します。I, C, Fのような格子点を複数もつ複合格子は他の結晶 系のPに変換できます。
課題: ZnOの構造最適化計算
- ZnO_qe.zipをダウンロードして実行し、ecutwfcを変えてscf計算を行い エネルギーの精度を確認する(単位を必ずかくこと)。
- 格子と原子位置の構造最適化計算を行う。構造最適化計算で、SCFループ と力のループを何度行ったか調べる。構造最適化で最終的に得られたエ ネルギーも記入すること。
- 収束した構造から格子定数a, b, c, α, β, γ を求める。
- 余裕があればhttp://www.crystallography.net/cod/search.html から計 算したい適当な結晶を探して構造最適化計算を行います。擬ポテンシャ ルはPseudo potentialから入手できます。
締切: 7月29日(月)10:00までに大窪(ohkubo.takahiro@faculty.chiba-u.jp)までemailにpdfファイルを添付して提出してください。メールの題名(Subject:)は以下のフォーマットを守ってください。添付ファイルのファイル名は自由ですがpdfファイルとしてください。
無機材料化学第4回レポート 19WM7777 山田純一
スペース、英数字はすべて半角文字としてください。ファイルは必ずpdfにして送ってください。
実習: バンド計算
課題: 適当な結晶構造の第一原理計算を行い電子密度を計算
- 提出期限: 8/3(金)の18:00
- 提出場所: 工学部1号棟204のレポート提出BOX
その他
動画の再生
動画はVMD+ffmpegを使ってmpeg-4フォーマットで作成しています。再生した い場合はVLC media playerをインストールして鑑賞してください。 https://www.videolan.org/vlc/index.ja.html 最新のFirefoxではブラウザ上でmpeg-4の動画を再生できるようです。
プログラミング
自分でプログラムを作成できれば、計算から得られ大量のデータを自由に解 析して必要な情報を引き出すことができます(Excelはすぐに破綻します)。 プログラム言語を習得して、実用的なアプリケーションを作成するまで、時 間がかかります。少しだけでもプログラムをかじりたいという人には、 python言語の習得をおすすめします。python言語と数値計算用のライブラリ numpyの使い方を覚えたら、相当広範囲な問題をカバーできます。大窪担当 のコンピュータ処理を受講すれば、一通りの技術を身につけることができま す。
http://chem.tf.chiba-u.jp/gacb10/lecture.files/chem_computer/index.html
windows上でC言語環境を作成してプログラミングすることも可能です。超quick C言語講座
質問等
計算機の使い方や実際の応用等、質問があったら気軽に大窪に連絡 (ohkubo.takahiro@faculty.chiba-u.jp)してください。できるだけ応じます。 直接話をしたいる場合は、平日の17:00以降に研究室(1号棟206)に来てくだ さい。
資料へのアクセス
講義資料の一部は学内ネットワークからのみアクセスできます。