拡散係数の拡散時間依存性の測定
1 はじめに
自己拡散係数の拡散時間依存性を測定するための原理と手順を説明します。
2 拡散測定の原理
拡散係数(\(D\)), 磁場勾配(\(g\)), 磁気回転比(\(\gamma\))とすると位相変調による信 号強度\(I(g, \Delta)\) は以下の式に従います。論文
\[ I(g, \Delta) = I_0\exp \left[ -D\gamma^2\int_0^t \left( \int_0^u g(w)dw \right)^2 du \right] \]
どのようなパルスシーケンスを使っても上式を計算することで拡散による信号 減衰の式を導くことができます。パルス磁場勾配を使った場合、上の積分は以 下のようような関数形になります。 \[ I(g, \Delta) = I_0\exp\left(-D\gamma ^ 2g ^ 2\delta ^ 2\alpha\right) = I_0\exp\left(-Db\right) \]
ここで、\(\alpha\) は有限のパルス幅に由来する項です。二重積分を手で計算 するのはかなり面倒なので、pythonで積分を計算します。半sine型と矩形型の パルス磁場勾配でbppledとsteの信号減衰を計算するプログラムの例 (grad_phase.py)です。代表的な2つのパルスシーケンス(bppledとste)の説明 を以下に示します。
拡散係数の時間依存性についても簡単にまとめています。2017-06_report.pdf
2.1 bipolar pulse gradient stimulated echo(bppled) 論文
特徴は以下のとおり。
- bipolarのgradientを使うことで定在磁場勾配の影響を受けにくい
- 磁場勾配の印加で発生する渦電流によるスペクトルの歪みをledの間で消す。
- 縦磁化で拡散時間のほとんどを保持するのでT2が短くても測定できる。
2.2 stimulated echo 論文
特徴は以下のとおり。
- unipolarのgradientを使うことで定在磁場勾配の影響を受けやすい。
- 縦磁化で拡散時間のほとんどを保持するのでT2が短くても測定できる。
3 測定の手順
3.1 温度設定
拡散は温度に強く依存するので温度制御下で実験を行います。
3.2 オフセットの調整
観測するピークが中心にくるようオフセットを調整します。初めて測定する ときは、force_tuneをチェックします。
C:\Users\delta/Documents/delta/experiments/Chiba/Li2S-P2S5/7Li_singlepluse.ex2
3.3 パルス幅の調整
オフセット調整と同じシーケンスで、40usから48usくらいパルス幅を変えながら測定を行って\(\pi\) パルスを求めます。
C:\Users\delta/Documents/delta/experiments/Chiba/Li2S-P2S5/7Li_singlepluse.ex2
3.4 T1の測定
飽和回復(saturation recovery)法でT1を求めます。
3.4.1 荒くT1測定
- scans=1、tauを適当に4ポイントで荒くT1を測定する。
3.4.2 精密にT1測定
- 求めたT1から0.01*5*T1 から 5*T1の範囲で7ポイントのtauを作る。
- tauのリストに5*T1*1.2のtauを追加すして8ポイントのtauリストとする。
- relaxation_delayを5*T1*1.2に設定する。
- scans=8にする。
3.5 拡散係数(\(D\))の測定
bppledを使って\(g\) を可変で測定した2次元FIDデータ(test-1.jdf)を Delta上でFTして2次元のスペクトルを求めます。2次元のスペクトルデー タ(test-2.jdf)を保存します。Delta付属のフィッテングツールは積分で 強度が評価できないことや不明なバクがあるため自作のプログラムで解析 します。
測定データをasciiに変換して、パルスシーケンスのパラメータ(\(\delta\) や\(g\) 等)を読み込み減衰の式にフィッテングして\(D\) を求めます。jdfファ イルをasciiに変換するためにJEOL Delta付属の「convert.exe」を使いま す。DeltaをインストールしたディレクトリのGlobalに入っていたかと思 います。Deltaのインストールは http://amorphous.tf.chiba-u.jp/wiki/index.php?Delta を参照してくだ さい。「convert.exe」がImageMagickのconvert.exeを被っているので Delta付属の「convert.exe」は「delta_convert.exe」にrenameしてパス の通ったところに配置します。
3.5.1 積分強度の取得
\(g\) を変えて測定した2Dデータから信号強度を求めます。保存したデータ をjdf2integ.py に渡して指定した範囲のピーク強度を計算します。テス トーデータ(test-2.jdf)を解析してみます。
jdf2integ.py test-2.jdf
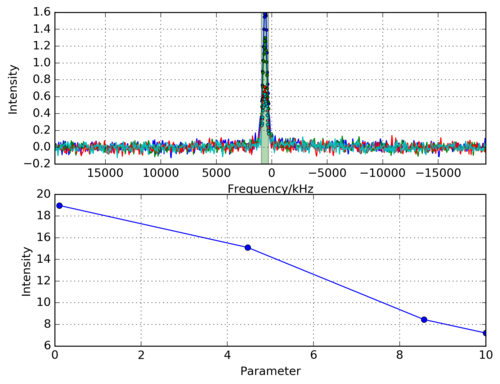
図を見ながらピークの積分範囲を確認します。この場合、892〜297くらい が適当でしょう。積分範囲を指定してもう一度、jdf2integ.py を実行すると 2つのグラフが画面に表示されます。
jdf2integ.py test-2.jdf -sx 897 297
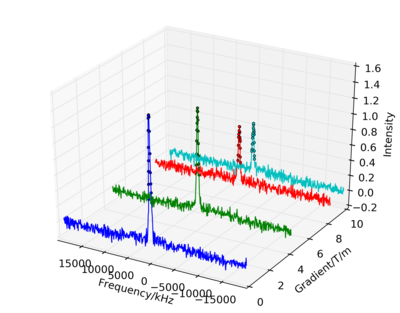
以下のコマンドで3次元プロットもできます。スペクトル上のマーカー が積分するデータです。
jdf2integ.py test-2.jdf -sx 897 297 -p 3d
また積分結果は、test-2.dat に以下のようなデータが保存されています。
# experiment "bpp_led.ex2"
# x_domain "7Li"
# delta_large 0.1[s]
# grad_1 1.6[ms]
# grad_1_shape "SINE"
# grad_pre 10[us]
# grad_post 0.5[ms]
# para. integ.
0.100000 18.980855
4.473030 15.105203
8.563640 8.453682
10.000000 7.204627
jdf2integ.py のオプションは以下のとおりです。
| option | 意味 | default |
|---|---|---|
| -h | ヘルプを表示 | |
| -xr | 表示の際にプロットするxの範囲 | 全部範囲 |
| -sx | 積分したいxの範囲 | 最大値1点 |
| -xl | x軸のラベル | Frequency |
| -zl | 3Dプロットした時のz軸のラベル | Intensity |
| -p | 2D(2d)か3D(3d)を指定します。 | 2d |
| -o | 出力するdatファイルのbasename | jdfのbasename |
| -nc | 中間ファイルascとhdrを削除しない | False |
| –xreverse | プロットするx軸をreverseする | True |
| -np | 図を表示しない (hoge.png等) | True |
| -op | 図を保存する場合のfile name (hoge.png等) | None |
積分範囲の指定は観測するピークの半分くらいが目安です。これでパルスパ ラメータ(\(g\) と\(\delta\))と\(D\) の目安がついたら次の拡散係数の拡散時間依存性の測定にす すみます。
3.5.2 強度変化から\(D\) の計算
jdf2integ.py で生成したtest-2.dat からフィッテングにより\(D\) を計算します。
dat2diffusion.py test-2.dat
標準出力に拡散時間(\(\Delta\)), \(I(0)\), \(D\) の結果が表示されます。
(DELTA, I0, D) = 0.100000, 19.217166, 2.326586e-12 +/- 5.276248e-12
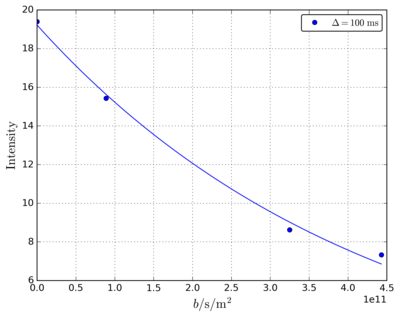
デフォルトで指数関数を使ってフィッテングして\(D\) を求めます。自然対数 をとって直線フィッテングしたい場合は以下のようにします。
dat2diffusion.py test-2.dat -t lin
拡散係数を求めるインプットファイル(datファイル)は複数できます。
dat2diffusion.py のオプションは以下のとおりです。
| option | 意味 | default |
|---|---|---|
| -h | ヘルプを表示 | |
| -d | 削除したデータポイントを複数指定します。 | [ ] |
| -t | 指数(lin)か直線(exPを指定します。 | exp |
| -np | プロットしない(データは出力する) | False |
3.6 拡散係数の拡散時間依存性(\(D(\Delta)\))の測定
拡散時間(\(\Delta\))を増やすことで減衰が大きくなります。信号の減衰は一 定にしたいので\(\Delta\) を増やしても減衰が一定になるよう\(D\), \(\delta\), \(\gamma\) から逆算してパルスシーケンスを作成します。ベース のシーケンスファイル(7Li_bppled.ex2)を準備してmake_diffseq.py で \(\Delta\) を変えたパルスシーケンスを生成します。測定データの保存先は、 常にdeltaの$HOMEになります。測定を終えたら測定データは、適時移動して 整理してください。以下の例は予想される\(D\) が\(2\times 10^{-10}\) m2/s で \(\Delta = 0.08\) msの\(D\) を測定する場合です。
make_diffseq.py 7Li_bppled.ex2 -D 0.08 -diff 2e-12
以下のような出力が得られます。
Gradient points: 10 Minimum I(gmax)/I(0): 0.20 Gradient list [T/m] 1: 0.100000 2: 1.716181 3: 2.985168 4: 3.945843 5: 4.806535 6: 5.636981 7: 6.480387 8: 7.378125 9: 8.386978 10: 9.613243
13T/mを越えたグラジエントは発生できまん。指定した条件で、\(g=13\) T/mになった場合はex2ファイルを生成しません。また最初の1点は必ず0.1 T/mとします。\(g\) のリストが良さそうだったらファイルに書き出します。-o でbasenameを指定します。
make_diffseq.py 7Li_bppled.ex2 -D 0.08 -diff 2e-12 -o test
ファイル名前は以下のとおりになります。
sequence名前 + basename + \(\Delta\).ex2
上のコマンドの場合は、「bppled_test-080ms.ex2」になります。
make_diffseq.py のオプション一覧は以下のとおりです。
| option | 意味 | default |
|---|---|---|
| -h | ヘルプを表示 | |
| -D | 測定したい拡散時間(\(\Delta\))をsで指定(必須) | |
| -diff | 予想される拡散係数(\(D\)) を m2 / sで指定(必須) | |
| -o | 出力するex2ファイルのベースネーム | None |
| –gpnt | \(g\) のポイント数 | 10 |
| –Imin | 最大の\(g\) で減衰する信号強度の割合(0.2なら20 % の信号減衰) | 0.2 |
\(\Delta\) を変えた一連のex2を生成したい場合は、シェル上でfor文を使え ば良いでしょう。以下は80msから200msまで50ms刻みで\(\Delta\) を変えた ex2ファイルを生成する例です。
for i in `seq 0.080 0.050 0.200`
do
make_diffseq.py 7Li_bppled.ex2 -D $i -diff 1.2e-10 -o hoge
done
これで以下の出力が得られます。
Gradient points: 10 Minimum I(gmax)/I(0): 0.20 Gradient list [T/m] 1: 0.100000 2: 1.716181 3: 2.985168 4: 3.945843 5: 4.806535 6: 5.636981 7: 6.480387 8: 7.378125 9: 8.386978 10: 9.613243 bppled_hoge-080ms.ex2 was created. Gradient points: 10 Minimum I(gmax)/I(0): 0.20 Gradient list [T/m] 1: 0.100000 2: 1.341955 3: 2.334230 4: 3.085423 5: 3.758434 6: 4.407796 7: 5.067290 8: 5.769270 9: 6.558135 10: 7.517004 bppled_hoge-130ms.ex2 was created. Gradient points: 10 Minimum I(gmax)/I(0): 0.20 Gradient list [T/m] 1: 0.100000 2: 1.138819 3: 1.980890 4: 2.618373 5: 3.189508 6: 3.740574 7: 4.300239 8: 4.895958 9: 5.565410 10: 6.379132 bppled_hoge-180ms.ex2 was created.
後は、生成したex2をどんどんsubmitすれば、\(D(\Delta)\) の測定ができ ます。得られたデータをFTしてスペクトルを保存しforを使って dat2diffusion.py で一気に解析すれば、\(D(\Delta)\) が得られます。