5. forとwhileによる繰り返し処理¶
「for」と「while」文を使って、指定した回数や指定した条件を満たす間、 繰り返し処理(ループ)を行うことができます。この回では「for」と「while」 文の使い方を身につけます。第5回講義の目的は以下のとおりです。
forとwhileによる繰り返し処理の文法を理解する。
forとwhileループ中で、breakとcontinueによる処理の分岐法を理解する。
for文¶
「 for 」の後に「 カウンタ変数 」「 in 」「 リスト変数 (オブジェクト) 」、最後に「 : 」を書いて改行します。ループ内の処 理はインデントでならべます。ループ内の処理はLISTの要素数だけ繰り替えさ れ、i にLISTの要素がループのたびに代入されます。
for i in LIST:
処理1
処理2
処理3
.
.
.
通常処理
.
.
.
「リスト変数」の型がリスト(オブジェクト)でない場合は、エラーになります。
for文を使って0から100までの整数を足してみます。
1total = 0 # totalの初期化
2for i in range(101): # range(101)で[0, 1, 2, ... 100]を生成
3 total = total + i # iはループ毎に0, 1, 2,...が代入される
4print("0+1+2+...+100={}".format(total))
if文と組み合わせて特定の条件を満たす数字のみの合計を求めてみます。
1total = 0
2for i in range(101):
3 if (i % 3) == 0:
4 total = total + i
5print("100までの数字で3で割りきれる数の合計は{}".format(total))
while文¶
「while」の後に「条件式」、最後に「:」を書いて改行します。ループ 内の処理はインデントでならべます。forと異なりリストの要素に連続アクセ スしないでループ処理する時に使います。ループ内の処理は、条件式を満たす 間(True)に繰り返されます。条件式を永遠に満たす場合、無限ループになって プログラムが終了しないので注意してください。後述するbreak文と組み合わ せてループを脱出させることができます。
while 条件式:
条件式がTrue時に実行する処理をインデントでならべる。
処理1
処理2
処理3
.
.
.
通常処理
.
.
.
1から99まで足しあげる例は以下のとおりです。
1i, total = 0, 0 # 変数の初期化
2while i < 100: # i<100の間、繰り返し
3 total = total + i # totalにiを足してupdate
4 i += 1 # iをupdate
5print(total)
6print(sum(range(100))) # 関数を使って同じ計算
for文で行う処理はwhile文で書き直すことができます。リストの要素に連続し てアクセスする処理を行う場合はfor文、条件式でループ回数を指定したい場 合はwhile文を使います。
1total = 0
2for i in range(100): # [0,...99]を作成
3 total = total + i # totalにiを足してupdate
4print(total)
5print(sum(range(100))) # 関数を使って同じ計算
ループのネスト¶
for文やwhile文で処理するループの中に、さらにfor文やwhile文を配置するこ とで多重のループ処理を行うことができます。九九の一覧を二重ループで表示 してみます。
1for i in range(10): # 10の位のループ
2 for j in range(10): # 1の位のループ
3 v = i * j # 九九の計算
4 print("{}*{}={}".format(i, j, i*j)) # 九九の結果を表示
注釈
多重ループのような繰り返し処理は、科学技術計算で頻出します。forや while文を使ったループ処理は、実行速度が遅いことが欠点です。高速にルー プ計算を行うために、後述するnumpyが開発されています。numpyを使って、 forやwhileによるループ計算をなるべく避けることがプログラムを高速化さ せるために重要になります。
ループ中での分岐処理¶
ループ処理中で、処理をスキップしたりループから脱出したい場合は、 continue文とbreak文が使えます。pass文は何もしない場合に使います。
命令文 |
意味 |
|---|---|
break |
break文のところでループから脱出する |
continue |
cotinue文以下の処理をスキップして次のループに進む |
pass |
何もしない。if, elseの分岐と組み合わせて使う |
while文で無限ループを作ってif文により分岐し、break文でループを脱出させることで、 0から50までの数字の合計を求めてみます。
1i, total = 0, 0 # 初期化
2while True: # 条件式がTrueなので無限ループ
3 total = total + i # totalにiを足してupdate
4 i += 1 # iに1を足してupdate
5 if i > 50: # iが51になったらループを脱出
6 break
7print(total)
8print(sum(range(51))) # range()とsum()を使って同じ計算
whileとfor文を使って1から100までの数字で20から50の数字を除いた合計を求 めてみます。
1total = 0 # 初期化
2for i in range(101):
3 if 20 <= i and i <= 50: # 20から50の範囲かの条件チェック
4 continue # 処理をスキップして次の要素へ
5 total = total + i # totalにiを足してupdate
6print(total)
7print(sum(range(20)) + sum(range(51, 101))) # range()とsum()を使って同じ計算
参考にifとelse、何もしないpassを使ってcontinueを書き換えることができます。continue文を使った方が直感的かと思います。
1total = 0 # 初期化
2for i in range(101):
3 if 20 <= i and i <= 50: # 20から50の範囲かの条件チェック
4 pass # 何もしない命令文のpass
5 else:
6 total = total + i # 条件を満たさない場合だけtotalをupdate
7print(total)
8print(sum(range(20)) + sum(range(51, 101))) # range()とsum()を使って同じ計算
要素番号の利用¶
forループで要素番号と要素を一緒に利用したい場合があります。 enumerate() を使うとすっきり書けます。
1x = [8.082, 9.962, 4.999, 6.642, 2.251, 8.082] # リストの定義
2# enumerate()を使って要素番号と要素を表示
3for i, xi in enumerate(x): # 要素番号をi、要素をxiに代入
4 print("{}番目のデータは{}".format(i, xi))
5
6# index()を使って要素番号と要素を表示
7for xi in x:
8 print("{}番目のデータは{}".format(x.index(xi), xi)) # 6番目が0番目になってしまうのでダメ
9
10# 面倒だが要素番号用のcntを定義して使う
11cnt = 0
12for xi in x:
13 print("{}番目のデータは{}".format(cnt, xi)) # 6番目が0番目になってしまう
14 cnt += 1
また要素数と同じxとyのリストの要素に同時にアクセスしたい場合、zip() 関数が使えます。
1x = [8.082, 9.962, 4.999, 6.642, 2.251]
2y = [0.328, 0.152, 2.089, 0.159, 0.233]
3# zipを使って計算
4for xi, yi in zip(x, y): # xiとyiに連続した要素を代入
5 print(xi + yi) # 各要素の足し算
6
7# enumerateを使って計算。zipを使った方が直感的
8for i, xi in enumerate(x):
9 print(x[i] + y[i]) # 各要素の足し算
内包表記¶
for文のルーブ処理が1行で、要素に処理を行って新しいリストを作りたい場合、 内包表記 が使えます。要素が文字のリストをfloatに変換したい場合、内包表 記を使わなければ以下のように書きます。
1l = ["13", "1.3e-2", "5.2", "2.4", "5.6", "3.2e10"] # 文字要素のリストを定義
2for i, d in enumerate(l): # enumerateで要素番号と要素にアクセス
3 l[i] = float(d) # リストの要素をupdate
4print(l)
内包表記を使えばすっきり書けます。
1l = ["13", "1.3e-2", "5.2", "2.4", "5.6", "3.2e10"] # 文字要素のリストを定義
2l = [float(d) for d in l ] # 各要素をfloat型へ
3print(l)
クイズ¶
Q1¶
0から100の整数の中で7で割りきれる整数の総和を求める。for文とwhile文の両方で作成する。
1# for文で作成
2total = 0 # totalの初期化
3for i in range(101):
4 if i % 7 == 0: # 7で割りきれるか調べる
5 total += i # totalをupdate
6print("forを使った結果: {:d}".format(total))
7
8# while文で作成
9i, total = 0, 0 # iとtotalの初期化
10while(i <= 100):
11 if i % 7 == 0:
12 total += i
13 i += 1 # iのupdate
14print("whileを使った結果: {:d}".format(total))
Q2¶
九九の表の中で5で割りきれる数字を表示する。
答え
1for i in range(1, 10): # 10の位
2 for j in range(1, 10): # 1の位
3 if i * j % 5 == 0: # 5で割りきれるかのチェック
4 print("{}*{}={}は5で割りきれる".format(i, j, i*j))
Q3¶
以下のリストを要素番号付きで表示する。
s = ["B", "Al", "Ga", "In", "Tl", "Uut"]
答え
1s = ["B", "Al", "Ga", "In", "Tl", "Uut"]
2for i, v in enumerate(s):
3 print("要素番号, 要素={}, {}".format(i, v))
Q4¶
以下のxとyのリストで、同じ要素番号の要素を足して作成したリストzを作る。
x = [0.56474832, 0.69283729, 0.12476153, 0.38224242, 0.10156261]
y = [0.44220529, 0.17673, 0.09141826, 0.7363728, 0.95426017]
答え
1x = [0.56474832, 0.69283729, 0.12476153, 0.38224242, 0.10156261]
2y = [0.44220529, 0.17673, 0.09141826, 0.7363728, 0.95426017]
3z = []
4for xi, yi in zip(x, y):
5 z.append(xi * yi)
6print(z)
Q5¶
0から1000までの数字で3のつく数字(3, 13, 31, 913等)の時に"ナベアツ"と表 示させる。str()とfind()を使ってください。
答え
1for i in range(101):
2 if str(i).find("3") != -1: # 文字型に変換して3が含まれるかチェック
3 print(i, "ナベアツ")
Q6¶
以下のデータから平均値 \(\overline{x}\) と分散 \(\sigma\) を求める。 \(\overline{x}\) と \(\sigma\) を求める式は以下のとおり。
glist = [1.05, 2.77, 1.14, 1.06, 1.57, 0.73, 2.42, 1.80, 0.18, 1.83,
1.40, 1.25, 1.76, 2.82, 0.33, 2.78, 2.42, 2.38, 2.90, 0.02,
1.36, 1.31, 0.93, 0.56, 0.08, 2.30, 0.86, 2.88, 0.00, 1.82,
0.29, 0.71, 1.17, 0.63, 2.04, 2.70, 1.95, 2.70, 1.17, 1.75,
1.42, 2.56, 0.76, 0.33, 0.91, 2.96, 0.71, 1.23, 2.91, 0.73]
答え
1glist = [1.05, 2.77, 1.14, 1.06, 1.57, 0.73, 2.42, 1.80, 0.18, 1.83,
2 1.40, 1.25, 1.76, 2.82, 0.33, 2.78, 2.42, 2.38, 2.90, 0.02,
3 1.36, 1.31, 0.93, 0.56, 0.08, 2.30, 0.86, 2.88, 0.00, 1.82,
4 0.29, 0.71, 1.17, 0.63, 2.04, 2.70, 1.95, 2.70, 1.17, 1.75,
5 1.42, 2.56, 0.76, 0.33, 0.91, 2.96, 0.71, 1.23, 2.91, 0.73]
6
7ave = sum(glist)/len(glist) # 平均値の計算
8std = 0 # 標準偏差の計算
9for v in glist:
10 std = std + (ave - v)**2
11std = std/len(glist) # Nで割って標準偏差を求める
12
13print("平均値: {:.3f}".format(ave))
14print("標準偏差: {:.3f}".format(std))
Q7¶
GPA=2.5以上の学生が何人いるか調べる。
glist = [1.05, 2.77, 1.14, 1.06, 1.57, 0.73, 2.42, 1.80, 0.18, 1.83,
1.40, 1.25, 1.76, 2.82, 0.33, 2.78, 2.42, 2.38, 2.90, 0.02,
1.36, 1.31, 0.93, 0.56, 0.08, 2.30, 0.86, 2.88, 0.00, 1.82,
0.29, 0.71, 1.17, 0.63, 2.04, 2.70, 1.95, 2.70, 1.17, 1.75,
1.42, 2.56, 0.76, 0.33, 0.91, 2.96, 0.71, 1.23, 2.91, 0.73]
答え
glist = [1.05, 2.77, 1.14, 1.06, 1.57, 0.73, 2.42, 1.80, 0.18, 1.83,
1.40, 1.25, 1.76, 2.82, 0.33, 2.78, 2.42, 2.38, 2.90, 0.02,
1.36, 1.31, 0.93, 0.56, 0.08, 2.30, 0.86, 2.88, 0.00, 1.82,
0.29, 0.71, 1.17, 0.63, 2.04, 2.70, 1.95, 2.70, 1.17, 1.75,
1.42, 2.56, 0.76, 0.33, 0.91, 2.96, 0.71, 1.23, 2.91, 0.73]
cnt = 0
for g in glist:
if g >= 2.5:
cnt += 1
print("GPA2.5以上の学生は{}人".format(cnt))
print("GPA2.5以上の学生は、{:.2f}%".format(cnt/len(glist)*100))
Q8¶
以下のxとyのデータを含む文字列から、x+yを計算する。zの結果をprint()で出力する。
ヒント
以下の手順でプログラムを作成する。
文字列dataの両端のスペースと改行コードを消す strip()
改行コード(\n)でsplit()して1行1要素とする。
x yの行はスキップしたforループで、split()しながらxとyの値をfloatに変換する。
zの計算をする。
data = """
x y
0.56474832 0.44220529
0.69283729 0.17673
0.12476153 0.09141826
0.38224242 0.7363728
0.10156261 0.95426017
"""
答え
data = """
x y
0.56474832 0.44220529
0.69283729 0.17673
0.12476153 0.09141826
0.38224242 0.7363728
0.10156261 0.95426017
"""
# 改行で分けたリストを作成, 1行目はx yなのでスキップ
lines = data.strip().split("\n")[1:]
for l in lines:
data = l.split()
x, y = float(data[0]), float(data[1])
z = x + y
print("{:.8f} + {:.8f} = {:.8f}".format(x, y, z))
Q9¶
AからJまでの点の三次元座標データを含む以下の文字列を考える。もっとも原 点に近い点を求める。
ヒント
以下の手順でプログラムを作成する。
問題8に習ってx, y, zのリストを作成する。また記号データを保持するリストもつくる。
forループで各点の原点からの距離を計算する。
forループの中でもっとも原点に近い座標の要素番号を調べる。
求めた要素番号から記号の表示
data = """
x y z
A 75.57 68.92 38.37
B 74.68 17.44 12.51
C 25.73 46.65 51.20
D 19.23 14.52 17.84
E 62.47 43.26 35.21
F 7.90 90.52 21.61
G 60.47 13.96 9.04
H 27.11 8.14 37.19
I 87.59 16.17 22.53
J 92.27 65.88 72.14
"""
答え(その1, 辞書データに保存してforで回して調べる)
data = """
x y z
A 75.57 68.92 38.37
B 74.68 17.44 12.51
C 25.73 46.65 51.20
D 19.23 14.52 17.84
E 62.47 43.26 35.21
F 7.90 90.52 21.61
G 60.47 13.96 9.04
H 27.11 8.14 37.19
I 87.59 16.17 22.53
J 92.27 65.88 72.14
"""
d = {}
for l in data.strip().split("\n")[1:]:
line = l.split()
symbol = line[0]
x = float(line[1])
y = float(line[2])
z = float(line[3])
r = (x**2 + y**2 + z**2)**0.5
d[symbol] = [x, y, z, r]
min_v, min_k = r, symbol
for k, v in d.items():
if min_v > v[3]:
min_v = v[3]
min_k = k
print("原点からもっとも近い記号: {}".format(min_k))
print("原点からもっとも近い距離: {:.2f}".format(min_v))
答え(その2, listを作成してindex()とmin()で調べる)
data = """
x y z
A 75.57 68.92 38.37
B 74.68 17.44 12.51
C 25.73 46.65 51.20
D 19.23 14.52 17.84
E 62.47 43.26 35.21
F 7.90 90.52 21.61
G 60.47 13.96 9.04
H 27.11 8.14 37.19
I 87.59 16.17 22.53
J 92.27 65.88 72.14
"""
xlist, ylist, zlist, rlist = [], [], [], []
symbollist = []
for l in data.strip().split("\n")[1:]:
line = l.split()
symbol = line[0]
x = float(line[1])
y = float(line[2])
z = float(line[3])
r = (x**2 + y**2 + z**2)**0.5
symbollist.append(symbol)
xlist.append(x)
ylist.append(y)
zlist.append(z)
rlist.append(r)
idx = rlist.index(min(rlist))
print("原点からもっとも近い記号: {}".format(symbollist[idx]))
print("原点からもっとも近い距離: {:.2f}".format(rlist[idx]))
Q10¶
以下の文章で"千葉"を含む行番号を表示させる。
ヒント
以下の手順でプログラムを作成する。
改行コードでsplit()してリストを作る。
forでループしながら1行毎に千葉が含まれるかチェックする。
s = """千葉大学は、1949年(昭和24年)に千葉医科大学・同附属医学専門部・同
附属薬学専門部・千葉師範学校・千葉青年師範学校・東京工業専門学校・千葉
農業専門学校を包括して新制の国立大学として発足した。国立大学法人法によ
り、2004年度には国立大学法人千葉大学となる。
新制国立大学として発足した当時は、5学部(医学部、園芸学部、学芸学部、
工学部、薬学部)から成り立っていたが、その後に学部研究科の拡充改組を重
ね、現在は10学部(国際教養学部、文学部、教育学部、法政経学部、理学部、
医学部、薬学部、看護学部、工学部、園芸学部)、11研究科(教育学研究科、
理学研究科、看護学研究科、工学研究科、園芸学研究科、融合科学研究科、人
文社会科学研究科、医学薬学府、専門法務研究科<法科大学院>、自然科学系研
究科アソシエーション)によって構成されるに至る。"""
答え
s = """千葉大学は、1949年(昭和24年)に千葉医科大学・同附属医学専門部・同
附属薬学専門部・千葉師範学校・千葉青年師範学校・東京工業専門学校・千葉
農業専門学校を包括して新制の国立大学として発足した。国立大学法人法によ
り、2004年度には国立大学法人千葉大学となる。
新制国立大学として発足した当時は、5学部(医学部、園芸学部、学芸学部、
工学部、薬学部)から成り立っていたが、その後に学部研究科の拡充改組を重
ね、現在は10学部(国際教養学部、文学部、教育学部、法政経学部、理学部、
医学部、薬学部、看護学部、工学部、園芸学部)、11研究科(教育学研究科、
理学研究科、看護学研究科、工学研究科、園芸学研究科、融合科学研究科、人
文社会科学研究科、医学薬学府、専門法務研究科<法科大学院>、自然科学系研
究科アソシエーション)によって構成されるに至る。"""
lines = s.split("\n")
for i, l in enumerate(lines):
if l.find("千葉") != -1:
print("{}行目は千葉を含む".format(i + 1))
Q11¶
以下の数値データは 関数 \(y=\frac{1}{3}x^2\) について、ランダムな \(x\) と \(y\) の値を文字列で定義したデータです。
data = """
# i x y
0 -2.1020 1.4729
1 -1.8776 1.1751
2 -0.9796 0.3199
3 -0.5306 0.0938
4 -0.5306 0.0938
5 -0.3061 0.0312
6 0.8163 0.2221
7 1.7143 0.9796
8 1.9388 1.2530
9 2.3878 1.9005
10 2.3878 1.9005
11 2.3878 1.9005
12 3.5102 4.1072
13 3.5102 4.1072
14 3.7347 4.6493
15 4.1837 5.8344
16 5.5306 10.1959
17 5.9796 11.9185
18 6.6531 14.7544
19 7.3265 17.8927
"""
数値データを読み込んで、データ \(x`の範囲で数値積分する。図のよう に各 :math:`x_i\) 点で矩形の幅と高さを求め、矩形の面積を足し合わせれば 良いです。矩形の幅は、\(x_i`毎に変わることに注意してください。比 較としてに :math:`x_0\) から \(x_{19}\) まで、関すを積分して求めた 数式から計算した解析解も計算しています。
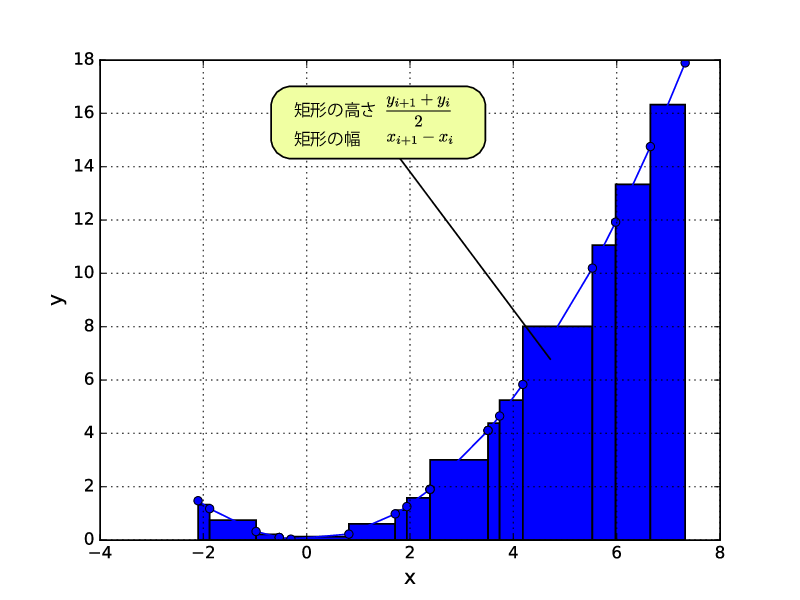
答えは次の通りになります。
矩形の近似解 = 45.16
積分式から求めた解析解 = 44.73
答え
data = """
# x y
-2.1020 1.4729
-1.8776 1.1751
-0.9796 0.3199
-0.5306 0.0938
-0.5306 0.0938
-0.3061 0.0312
0.8163 0.2221
1.7143 0.9796
1.9388 1.2530
2.3878 1.9005
2.3878 1.9005
2.3878 1.9005
3.5102 4.1072
3.5102 4.1072
3.7347 4.6493
4.1837 5.8344
5.5306 10.1959
5.9796 11.9185
6.6531 14.7544
7.3265 17.8927
"""
data = data.strip().split("\n")[1:]
x, y = [], []
for d in data:
dd = d.split()
x.append(float(dd[0]))
y.append(float(dd[1]))
area = 0
for i in range(0, len(x) - 1):
w = x[i + 1] - x[i]
h = 0.5*(y[i] + y[i+1])
area += w * h
print("矩形の近似解 = {:.2f}".format(area))
ans = (7.3265**3 - (-2.1020)**3)/9
print("積分式から求めた解析解 = {:.2f}".format(ans))