2017年度テスト

以下のコンテンツは2017年度のものです。2018年度は筆記試験とします。

成績評価の内訳

出席やレポートも加味して成績評価を行います。

項目

点数

出席

25 \(\pm\) 10

講義中の課題(3回分)

15 \(\pm\) 5

最終課題

60 \(\pm\) 10

なお講義に積極的だった人や鋭い質問をした人には、上の配点に加えて最大10 点程度のボーナス点が加算されます。

成績評価の考え方

成績評価はレポートとします。プログラムを作成する課題のため、正しく動く か動かないかのどちらかになるため、学生間で点数差をつけることができませ ん。そのため、 提出順序で傾斜配点 とします。傾斜配点ですが、課題の 解法情報が拡散によって学生間に伝達すると考えました。 \(x=0, t=0\) で発生した情報は、以下の確率分布関数(正規分布) \(P(x, t)\) によっ て周囲に広がっていくと仮定します。

\[P(x, t) = \frac{1}{2\sqrt{\pi Dt}}\exp\left(-\frac{x^2}{4Dt}\right)\]

ここで \(D\) は拡散係数です。 \(D=1\) として \(t\) を変え て、この関数をプロットしてみると時間とともに遠くまで情報が伝達することがわかります。

example-01
import numpy as np
import matplotlib.pyplot as plt

def func(x, D, t):
    y = 1/(2*np.sqrt(np.pi * D * t)) * np.exp(-(x**2)/(4*D*t))
    return y

xr = (-50, 50)
x = np.linspace(xr[0], xr[1], 1000)
D = 1
fig, ax = plt.subplots()
ax.plot(x, func(x, D, 1), label="$t={}$".format(1))
ax.plot(x, func(x, D, 2), label="$t={}$".format(2))
ax.plot(x, func(x, D, 5), label="$t={}$".format(5))
ax.plot(x, func(x, D, 10), label="$t={}$".format(10))
ax.plot(x, func(x, D, 20), label="$t={}$".format(20))
ax.plot(x, func(x, D, 50), label="$t={}$".format(50))
ax.plot(x, func(x, D, 100), label="$t={}$".format(100))
ax.legend(loc="best")
ax.set_xlabel("$x$")
ax.set_ylabel("$P(x)$")
ax.set_xlim(xr)
fig.savefig("diffusion.png")
plt.show()
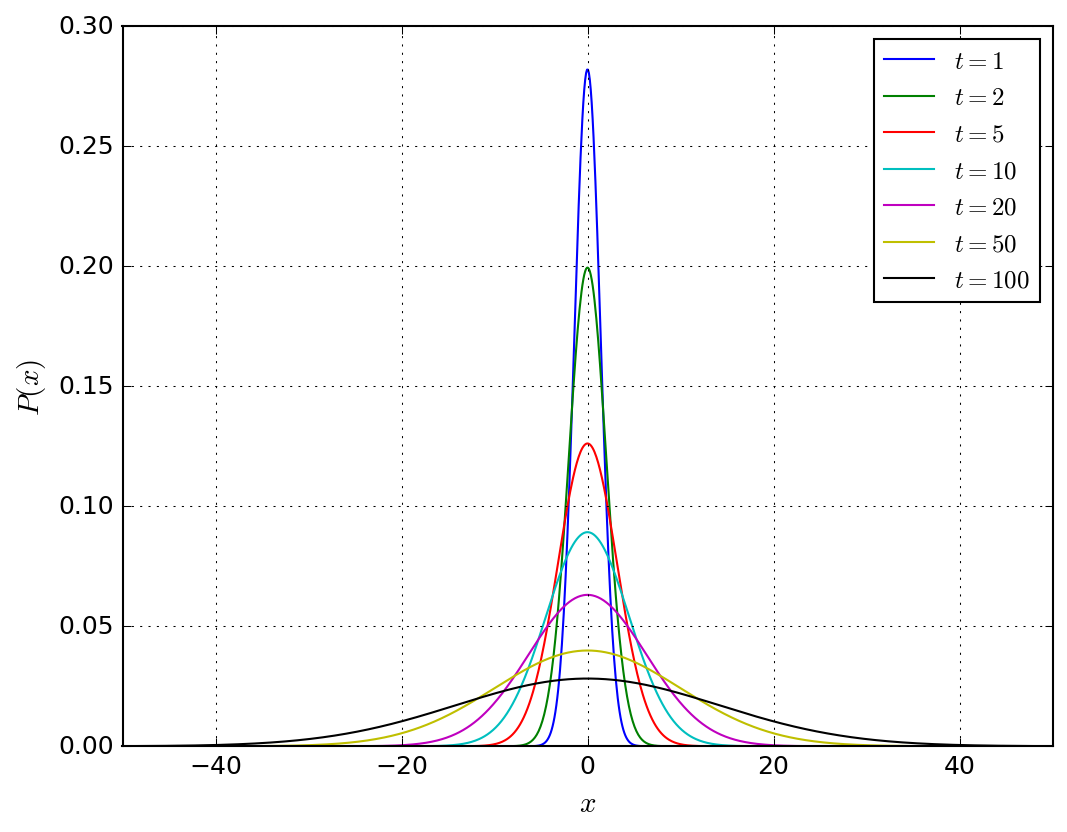
../_images/diffusion.png

時間と平均距離の関係を求めてみます。

\[\overline{x(t)} = \frac{1}{N}\sum_i^N \sqrt{x_i^2(t)} = \sqrt{ \frac{\int_{-\infty}^{\infty}x^2P(x,t)dx} {\int_{-\infty}^{\infty}P(x,t)dx}}\]

右項のルートに入っている分母は確率分布関数の積分なので1になりますし、分母はいわゆるgauss積分で解析解が得られますが、あえてsympyパッケージを使って代数計算してみます。

example-02
 1from sympy import *
 2
 3# tとDは負だと発散するので positiveだけ
 4t, D = symbols("t, D", positive=True)
 5x = symbols("x")
 6term1 = x**2/(2*sqrt(pi*D*t)) * exp(-(x**2/(4*D*t)))
 7term2 = 1/(2*sqrt(pi*D*t)) * exp(-(x**2/(4*D*t)))
 8term1_int = integrate(term1, (x, -oo, oo),)
 9term2_int = integrate(term2, (x, -oo, oo),)
10g = sqrt(term1_int/term2_int)
11print("x-bar = ", g)

次のような平均変位と時間の関係(いわゆるEinsteinの式)が得られます。

x-bar =  sqrt(2)*sqrt(D)*sqrt(t)
\[\overline{x(t)} = \sqrt{2Dt}\]

\(\sqrt{t}\) と \(\overline{x}\) の関係について \(D\) を変えてプロットしてみます。大雑把に一定の \(t\) で情報が伝達するとして、最初に提出した \(t=0\) の学生を10点するため適当に係数をかけて、履修登録している52人分の相対評価を行うこととします。

example-03
import numpy as np
import matplotlib.pyplot as plt


def f(t, D):
    return np.sqrt(2 * D * t)


fig, ax = plt.subplots()
t = np.linspace(0, 51, 52)
x = np.empty((t.size, 3))
x[:, 0] = f(t, 10)  # D = 10
x[:, 1] = f(t, 20)  # D = 20
x[:, 2] = f(t, 40)  # D = 40

ax.plot(t, x[:, 0], "-", label="$D=10$")
ax.plot(t, x[:, 1], "-", label="$D=20$")
ax.plot(t, x[:, 2], "-", label="$D=40$")
ax.set_xlabel("$\sqrt{t}$")
ax.set_ylabel("${\\rm (solid\ line)},\ \overline{x}$")
ax.legend(loc="best")
ax.set_ylim(0, 80)
bx = ax.twinx()
bx.plot(t, 0.1*(100 - x[:, 0]), "--", label="$D=10$")
bx.plot(t, 0.1*(100 - x[:, 1]), "--", label="$D=20$")
bx.plot(t, 0.1*(100 - x[:, 2]), "--", label="$D=40$")
bx.grid()
bx.set_ylim(3, 10.5)
bx.set_ylabel("${\\rm score\ (dotted\ line)},\ 0.1(100-\overline{x})$")

# data save
o = open("score.dat", "w")
o.write("{:>10s}".format("rank"))
o.write("{:>10s}".format("D=10"))
o.write("{:>10s}".format("D=20"))
o.write("{:>10s}".format("D=40"))
o.write("\n")

for i, ti in enumerate(t):
    if i % 10 == 0:
        o.write("-" * 50 + "\n")
    o.write("{:10.0f}".format(ti + 1))
    o.write("{:10.1f}".format(0.1*(100 - x[i, 0])))
    o.write("{:10.1f}".format(0.1*(100 - x[i, 1])))
    o.write("{:10.1f}".format(0.1*(100 - x[i, 2])))
    o.write("\n")
fig.savefig("score.png")
plt.show()
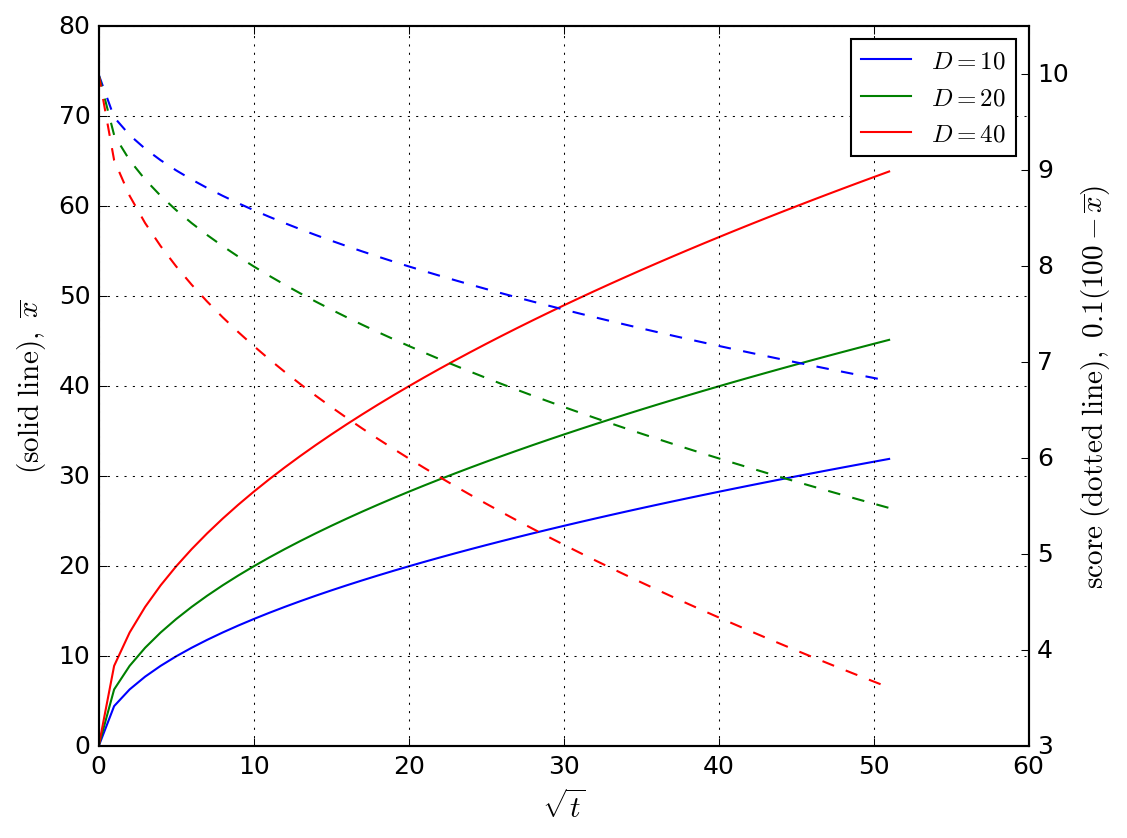
../_images/score.png

プロットした結果に基づいて課題1問あたりの提出順位と点数は以下のとおりです。

      rank      D=10      D=20      D=40
--------------------------------------------------
         1      10.0      10.0      10.0
         2       9.6       9.4       9.1
         3       9.4       9.1       8.7
         4       9.2       8.9       8.5
         5       9.1       8.7       8.2
         6       9.0       8.6       8.0
         7       8.9       8.5       7.8
         8       8.8       8.3       7.6
         9       8.7       8.2       7.5
        10       8.7       8.1       7.3
--------------------------------------------------
        11       8.6       8.0       7.2
        12       8.5       7.9       7.0
        13       8.5       7.8       6.9
        14       8.4       7.7       6.8
        15       8.3       7.6       6.7
        16       8.3       7.6       6.5
        17       8.2       7.5       6.4
        18       8.2       7.4       6.3
        19       8.1       7.3       6.2
        20       8.1       7.2       6.1
--------------------------------------------------
        21       8.0       7.2       6.0
        22       8.0       7.1       5.9
        23       7.9       7.0       5.8
        24       7.9       7.0       5.7
        25       7.8       6.9       5.6
        26       7.8       6.8       5.5
        27       7.7       6.8       5.4
        28       7.7       6.7       5.4
        29       7.6       6.7       5.3
        30       7.6       6.6       5.2
--------------------------------------------------
        31       7.6       6.5       5.1
        32       7.5       6.5       5.0
        33       7.5       6.4       4.9
        34       7.4       6.4       4.9
        35       7.4       6.3       4.8
        36       7.4       6.3       4.7
        37       7.3       6.2       4.6
        38       7.3       6.2       4.6
        39       7.2       6.1       4.5
        40       7.2       6.1       4.4
--------------------------------------------------
        41       7.2       6.0       4.3
        42       7.1       6.0       4.3
        43       7.1       5.9       4.2
        44       7.1       5.9       4.1
        45       7.0       5.8       4.1
        46       7.0       5.8       4.0
        47       7.0       5.7       3.9
        48       6.9       5.7       3.9
        49       6.9       5.6       3.8
        50       6.9       5.6       3.7
--------------------------------------------------
        51       6.8       5.5       3.7
        52       6.8       5.5       3.6

課題の提出方法

作成したプログラムは、指定したURLに接続してファイルをuploadしてくださ い。フォーマットに従ったファイル名でuploadする必要があります。提出用の URLとパスワードを大学のメールアドレスに送信するので各自確認するようし てください。

Subject: コンピュータ処理 最終課題提出用のURL
To: 10T0000Z@chiba-u.jp
From: =?iso-2022-jp?b?GyRCQmc3JhsoQiAbJEI1Lk1OGyhC?= <ohkubo.takahiro@faculty.chiba-u.jp>
Body: 最終課題提出用のURLとパスワードをお知らせます。

http://amorphous.tf.chiba-u.jp/lecture/comp/report/upload.cgi?user=10T0000aaaaaaa
password: 537ReR

URLに接続し作成したプログラムをuploadしてください。
プログラムのファイル名は以下のフォーマットに従ってください。

10T0000Z-Q1.py

Q1は課題番号です。
ファイル名はすべて半角英数文字です。
フォーマットに従っていないとuploadできません。
全角文字は使わないで下さい。

問題は2/7(水)10:00に提示します。提出締切りは2/13(火)10:00です。
課題のURL
http://chem.tf.chiba-u.jp/gacb10/lecture.files/chem_computer/17/17.html#id5

--------------------------------------------------
担当: 大窪 <ohkubo.takahiro@faculty.chiba-u.jp>

パスワードは他人に見られないよう管理してください。同じ課題のプログラム を何度提出しても構いませんが、最後に提出されたプログラムと提出時間で評 価します。なおメール等での提出は認めません。

最終課題

問題は2/7(水)10:00に表示します。質問があれば応じますが、情報共有のため このページで質問の回答をお知らせします。提出順位で評点を変えるので、で きた問題から順次提出してください。再提出も可能ですが、最後に提出したファ イルで評価します。提出期限は以下のとおりとします。提出期限を過ぎると uploadできなくなります。

  • 2/13(火) 10:00

学生同士で相談してプログラムを作成するのはかまいませんが、丸々コピペの プログラムを提出することは止めてください。コメント文を除いて、丸々コピ ペしていないかチェックします。間違い方(もしくは高度な解法)まで同じよう なプログラムを発見しコピーが疑われる場合は、2/15(木)に呼び出して口頭試 問することとします。2/15(木)に来れない、または連絡がつかない場合は未提 出扱いとします。

正しく動かないプログラムを提出しても未提出扱いです。 問題は出力結果付き で提示します。自分で作ったプログラムが出力結果と同じになることを確認し てから提出してください。

問題1(課題番号Q1)

水素原子の電子のエネルギー(n=1, 2, 3, 4)を以下の式にしたがって計算するプログラムを作成する。

\[\begin{split}&E = -\frac{m_e e^4}{8\epsilon_0^2n^2h^2} \times 10^{-3} \times N_A \quad {(\rm kJ/mol)}\\ &電子の質量 m_e = 9.1094\times 10^{-31}\quad ({\rm kg})\\ &電気素量 e = -1.6022\times 10^{-19}\quad ({\rm C})\\ &真空の誘電率 \epsilon_0 = 8.85419 \times 10^{-12}\quad ({\rm F/m})\\ &プランク定数 h = 6.6261 \times 10^{-34}\quad ({\rm J\cdot s})\\ &アボガドロ数 N_A = 6.0221 \times 10^{23}\quad ({\rm mol^{-1}})\\\end{split}\]

print文を使って次と同じフォーマットで出力させること。

n=1: -1312.81 [kJ/mol]
n=2:  -328.20 [kJ/mol]
n=3:  -145.87 [kJ/mol]
n=4:   -82.05 [kJ/mol]

問題2(課題番号Q2)

1から100000までの整数で、3と13で割りきれる数字の平均値と個数を求めるプログラムを作成する。

print文を使って次と同じフォーマットで出力させること。

3と13で割りきれる数字の個数: 2564
3と13で割りきれる数字の平均値: 50017.5

問題3(課題番号Q3)

点数と名前のデータが保存されているファイル(q3.dat)から、90点以上の名前をリストアップする。90点以上の点数で平均値を求め点数の高い順番で表示するプログラムを作成する(架空の名前です)。q3.datを読み込んで処理すること。q3.datの中身をエディターで変更してはならない。

print文を使って次と同じフォーマットで出力させること。

90点以上の平均: 95.6点
90点以上のリスト
99.70点: ブムニョ ゴヒカ
98.67点: ビウェリョミャト ヴィチャサリャピョ
98.40点: ミャジョホジョヤ ブジェペザニャ
98.19点: ロチョカナ ビュオモト
96.78点: カティビツィフェ メボザビョヨ
95.75点: ジェゲ－ジャ ツァピュツィウォ
95.46点: ズト ビュギュ
92.02点: キャ－ パヂ
91.30点: ゾチュ リニュ
90.19点: ンニャジェ ピャコカ

質問に対する回答

[質問]点数と名前のペアをソートすることができません。

[回答]順位のリストを独立したデータとして作ると良いと思います。numpyを使うならば、np.argsort()で点数の順番の入ったリストを取得するのがスマートです。

問題4(課題番号Q4)

スタートからゴールまでのマス目が300個あるすごろくを考える。疑似乱数に よってサイコロをふり、ゴールするために必要なサイコロを振る回数を求める。なお、ゴールのマ ス目にぴったり到達した時だけゴールとなる。ゴールを越えたサイコロの目 がでた場合、越えた分だけゴールから遠ざかることとする(下図参照)。

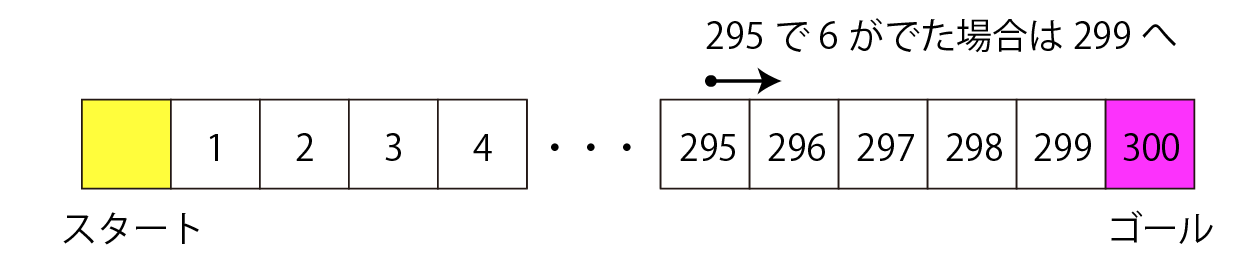
../_images/q4.png

サイコロの目は、疑似乱数により次の方法で発生させることとします。

import random
random.seed(333)
n = random.choice([1, 2, 3, 4, 5, 6])

計算結果はprint文を使って次と同じフォーマットで出力させること。

最後のサイコロの目: 2
サイコロを振った数: 94回

質問に対する回答

[質問]何回サイコロを振るかがわかっていない中でどのように方針を立てるべ きなのかが全く思いつきません。

[回答]forかwhileで無限loopを作ってサイコロを振ってコマをすすめつつ、ゴー ルする条件になったらbreakするのが良いかと。

[質問]seedを指定しているので毎回同じ数字が出るのですが、　これでよいの でしょうか。それとも提出されたものの動作確認のために　あえてそうしてい らっしゃるのでしょうか。

[回答]seedを指定しないと、同じ乱数が生成されないので、私の示している結 果と異なってしまいます。動作確認のためです。

[質問]同じフォーマットで出力させよとありますが、全く同じような答えでないといけないのでしょうか。

[回答]同じフォーマットでなく答えが正しい場合、減点です。答えがまったく違っていたら0点です。

[質問]知恵袋に問4番と同じ質問がありました。

https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q13185825338

[回答]質問内容と日付をみて、受講者が質問していることは間違いないようです。低レベルな学生が間違って入学してしまっているようです。

注意喚起をメールで受講者に流すと、投稿した本人が削除依頼を出したためかリンク切れになっていました。screen shotを保存しています。

../_images/screen_shot.png

問題5(課題番号Q5)

溶融したNaClのxyzファイル(NaCl-melt.xyz)から、原子間距離がもっとも近いNaとClのペアをピックアップし、NaとClのxyz座標と距離を表示する。計算結果はprint文を使って次と同じフォーマットで出力させること。

最近接の距離: 1.91
最近接の原子座標
Na: [14.1819 53.0853 43.6657]
Cl: [15.9638 52.562  43.2295]

質問に対する回答

[質問]差のデータは2048×2048個出てくると思われますが、for文などでどの ように算出していけばいいのかがわかりません。

[回答]全部のNaについて、forで1つのNaと全部のClの距離を求めつつ、2048×2048の距離の表をnumpyのbroadcastで作成するのはどうでしょうか。

[質問]最近接の距離は出せたのですが、原子座標を表示させることができないので、方針など教えていただけないでしょうか?

[回答]いろんなやり方があるかと思いますが、最短距離を計算する際に原子座標を一緒に保存しておけばよいかと思います。距離のリストをもっているなら、最小距離のindexから原子ペアを推定できるかと思います。

[質問]よく意図するところがわからない質問があった。

[回答]numpyを利用することをアドバイスした。

this.py
1import numpy as np
2
3data = np.loadtxt("NaCl-melt.xyz", skiprows=2, dtype=object)
4Na = data[data[:, 0] == "Na", 1:4].astype(float)
5Cl = data[data[:, 0] == "Cl", 1:4].astype(float)

問題6(Q1: 締切は2/5(火)17:00)

トルエンのxyzファイル(Toluene.xyz)から次の操作を行ってToluene-rotate.xyzを作成する。操作2は内積の公式を利用して角度を求めますが、難しいのでスキップしても良いです。

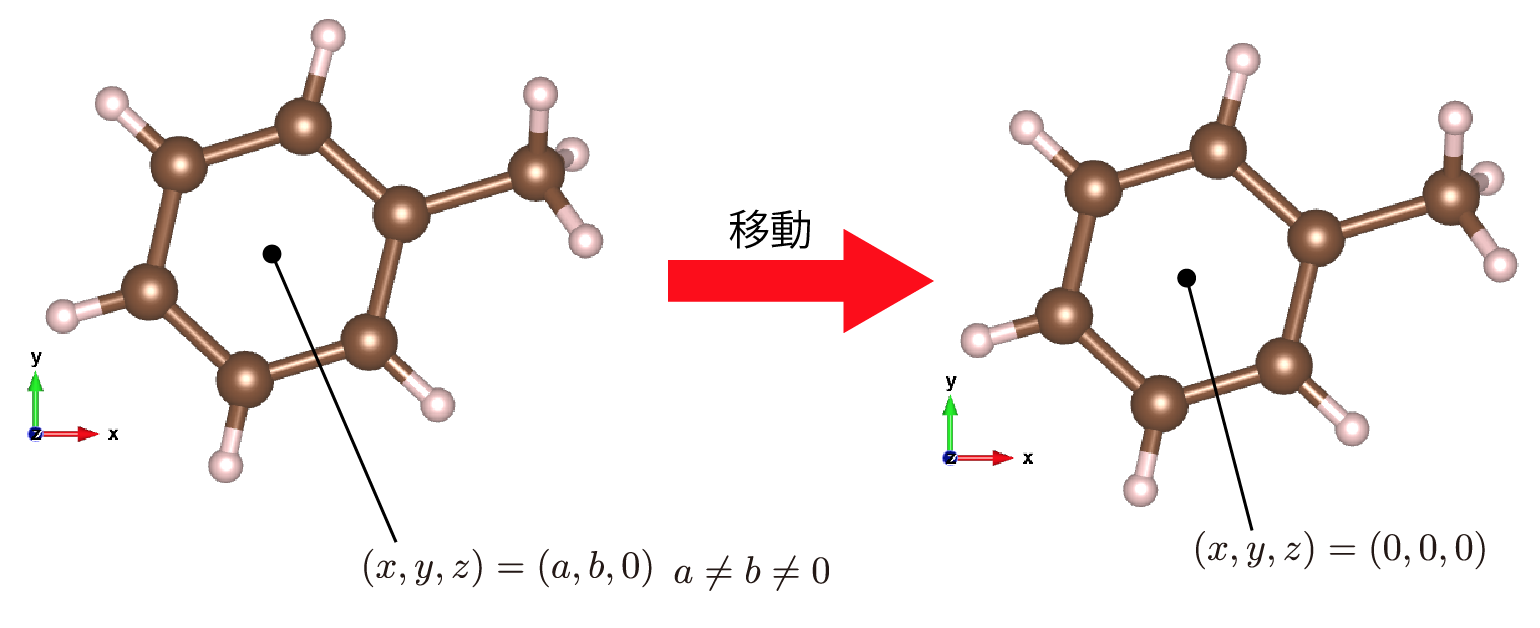
  • 六員環を構成するC原子の重心が(x, y, z) = (0, 0, 0)になるよう移動する。手動で六員環のCを選択しても良いですが、プログラムでCを抜き出して選択するとより良いです(C-C結合2個C-H結合1個 または C-C結合3つのCが六員環のC)。(操作1)

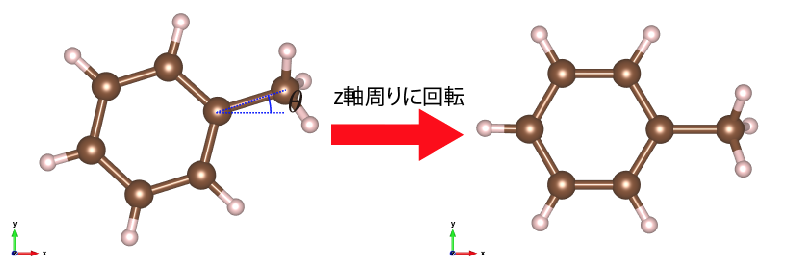
  • CH3のCと六員環のCの結合がx軸に平行になるようz軸まわりに \(\theta\) だけ 回転させる。(操作2)

  • z方向に3Ang.シフトさせながら-60度(軸方向右ネジが＋の角度)ずつ回転させた構造を6つ作る。(操作3)

操作1

../_images/q6-1.png

操作2

../_images/q6-2.png

操作3

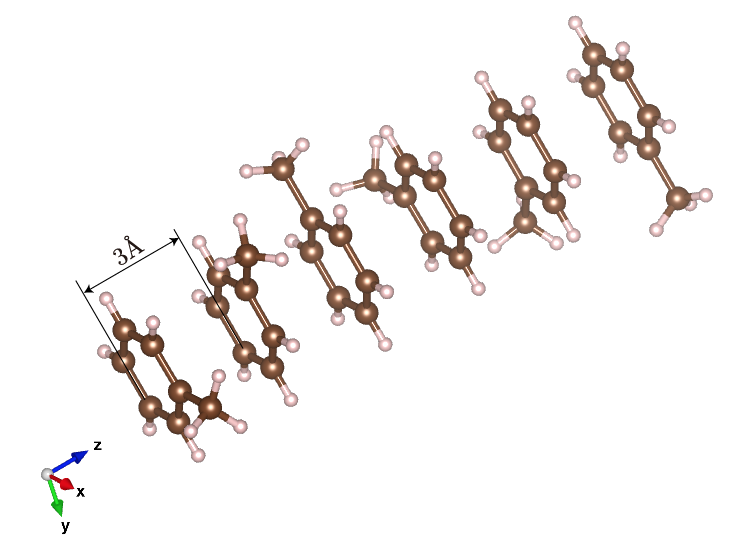
../_images/q6-3.png

作成した構造は、以下と同じフォーマットでToluene-rotate.xyzとして保存する。

Toluene-rotate.xyz

質問に対する回答

[質問]軸の中心への合わせ方がわかりません。

[回答]Cのxとyの平均値から重心座標を求めます。後は、重心位置の座標で全原子を平行移動するだけ。

[質問]六員環に含まれない炭素原子は座標から自分で判別してよいのでしょう か。

[回答]六員環に含まれない炭素原子をvestaで確認し、自分で判別してかまい ません。Hが3つくっついているCを探すようプログラムするとより良いです。

[質問]重心が原点に移動しているのか確かめたところ、　計算結果が 1.4802973661668753e-16となってしまいました。

[回答]これは桁落ちのためで0と同じです。e-16は \(10^{-16}\) と同じ意味です。

[質問]角度を求めてからの原子の回転の仕方がわかりません。

[回答]回転行列を使って原子を軸まわりに回転させてください。

http://chem.tf.chiba-u.jp/gacb10/lecture.files/chem_computer/11/11.html#id50